Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cần tìm là x.
+ Một nửa của x trừ đi một nửa đơn vị rồi nhân với một nửa của x là:
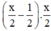
Theo bài ra ta có phương trình:
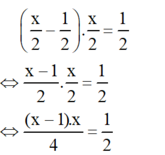
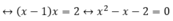
Có a = 1; b = -1; c = -2
⇒ a – b + c = 1 – (-1) – 2 = 0
⇒ Phương trình có hai nghiệm x 1 = - 1 ; x 2 = 2 .
Vậy số cần tìm là -1 hoặc 2.
Kiến thức áp dụng
Để giải bài toán bằng cách lập phương trình ta làm theo các bước:
Bước 1: Lập phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn tất cả các đại lượng khác qua ẩn vừa chọn.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Đối chiếu điều kiện rồi kết luận.

Gọi số phải tìm là x.
một nửa của nó trừ đi một nửa đơn vị là: -
Theo đầu bài ta có phương trình: =
hay x2 – x – 2 = 0, có a – b + c = 1 – (-1) – 2 = 0 nên: x1 = -1, x2 = 2
Trả lời: Số phải tìm bằng -1 hoặc 2.
Gọi số phải tìm là x.
một nửa của nó trừ đi một nửa đơn vị là: -
Theo đầu bài ta có phương trình: =
hay x2 – x – 2 = 0, có a – b + c = 1 – (-1) – 2 = 0 nên: x1 = -1, x2 = 2
Trả lời: Số phải tìm bằng -1 hoặc 2.

Gọi tử là: x
mẫu là: y\(\left(y\ne0\right)\)
\(\Rightarrow x+y=32\left(1\right)\)
Vì khi tăng mẫu thêm 10 đơn vị và giảm tử đi 1 nửa thì được phân số mới bằng \(\frac{2}{17}\)
\(\Rightarrow\frac{x.0,5}{y+10}=\frac{2}{17}\Leftrightarrow8,5x-2y=20\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\hept{\begin{cases}x+y=32\\8,5x-2y=20\end{cases}\Leftrightarrow\hept{\begin{cases}x=8\\y=24\end{cases}}}\)
\(\Rightarrow\)Phân số cằn tìm là: \(\frac{8}{24}=\frac{1}{3}\)

Gọi chiều dài miếng bìa là
\(x\left(cm;x>4\right)\)
Chiều rộng miếng bìa là:
\(\frac{3x}{5}\left(cm\right)\)
Diện tích ban đầu là:
\(\frac{x\times3}{5}=x^2\times\frac{3}{5}\left(cm^2\right)\)
Diện tích mới của miếng bìa là:
\(\left(x-4\right)\times\left(\frac{3x}{5}-1\right)=\frac{1}{2}\times x^2\times\frac{3}{5}\Leftrightarrow x=10\)
Chu vi miếng bìa đó là:
\(2\times\left(10+\frac{3}{5}\times10\right)=32\left(cm\right)\)
Đáp số: 32 (cm)

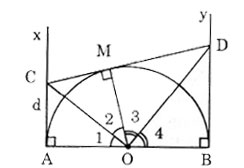 a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = CA; DM = DB;
∠O1 = ∠O2; ∠O3 = ∠O4
⇒ ∠O2 + ∠O3 = ∠O1 + ∠O4 = 1800/2 = 900 (tính chất hai tia phân giác của hai góc kề bù).
⇒ ∠OCD = 900
b) CM và CA là hai tiếp tuyến của đường tròn, cắt nhau tại C nên CM = CA
Tương tự:
DM = DB
⇒ CM + DM = CA + DB
⇒ CD = AC + BD.
c) Ta có OM ⊥ CD
Trong tam giá vuông COD, OM Là đường cao thuộc cạnh huyển
OM2 = CM.DM
Mà OM = OA = OA = AB/2 và CM = AC; DM = BD
Suy ra AC.BD = AB2/2 = không đổi

Gọi số cần tìm là x.
+ Một nửa của x trừ đi một nửa đơn vị rồi nhân với một nửa của x là:
Theo bài ra ta có phương trình:
Có a = 1; b = -1; c = -2
⇒ a – b + c = 1 – (-1) – 2 = 0
⇒ Phương trình có hai nghiệm x1 = -1; x2 = 2.
Vậy số cần tìm là -1 hoặc 2.
Kiến thức áp dụng