Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
OA2=42+32
=16+9=25
Suy ra OA= 5(m)
* OC2=62+ 82=36+64=100
=> OC =10(m)
* OB2=42+62=16+26=52
=> OB=√52 ≈ 7,2(m)
* OD2=32+82=9+64=73
=>OD= √73 ≈ 8,5(m)
Nên OA=5<9; OB≈7,2<9
OC=10>9; OD≈8.5<9
Như vậy con cún có thể đi tới các vị trí A,B,D nhưng không đế được vị trí C

Ta có:
OA2=42+32
=16+9=25
Suy ra OA= 5(m)
* OC2=62+ 82=36+64=100
=> OC =10(m)
* OB2=42+62=16+26=52
=> OB=√52 ≈ 7,2(m)
* OD2=32+82=9+64=73
=>OD= √73 ≈ 8,5(m)
Nên OA=5<9; OB≈7,2<9
OC=10>9; OD≈8.5<9
Như vậy con cún có thể đi tới các vị trí A,B,D nhưng không đế được vị trí C

Áp dụng định lý Py-ta-go , ta có :
OA2 = 42 + 32 = 16 + 9 = 25
=> OA = 5
=> OA < 9
OB2 = 62 + 42 = 36 + 16 = 52
=> OB = √52
=> OB < 9
OC2 = 62 + 82 = 36 + 64 = 100
=> OC = 10
=> OC > 9
OD2 = 32 + 82 = 9 + 64 = 73
=> OD = √73
=> OD < 9
Vậy chú Cún có thể đến được các điểm A,B,D và không đến được điểm C
Bài 1 Đố: Trong lúc anh Nam dựng tủ cho đứng thẳng, tủ vướng vào trần nhà không?

Gọi x là đường chéo của tủ. h là chiều cao của nhà. h= 21dm.
Ta có x2 = 202 + 42 = 400 + 16 = 416.
=> x = √416 (1)
Và h2 =212 = 441, => h = √441 (2)
So sánh (1) và (2) ta được x < h.
Như vậy anh Nam đẩy tủ đứng thẳng không bị vướng vào trần nhà.
Bài 2 : Trên giấy kẻ ô vuông ( độ dài cạnh ô vuông bằng 1 ) , cho tam giác ABC như hình 114 . Tính độ dài mỗi cạnh của tam giác ABC .

Áp dụng định lý Py-ta-go , ta có :
AB2 = 22 + 12 = 4 + 1 = 5
=> AB = √5
AC2 = 32 + 42 = 9 + 16 = 25
=> AC = 5
BC2 = 52 + 32 = 25 + 9 = 34
=> BC = √34
Vậy ...
Gửi bn bê trần ( chúc bn hc tốt )

Ta có:
\(AC+BC\ge AB\) ( vì \(C\)là điểm chưa xác định )
Do đó:
\(AC+BC\)ngắn nhất khi:
\(AC+BC=AB\)
\(\Rightarrow C\)nằm giữa \(AB\)
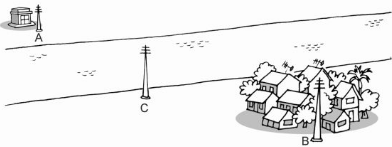
Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây ngắn nhất là \(C\)nằm giữa \(AB\)
Ta có: AC + BC ≥ AB ( vì C là điểm chưa xác định)
Do đó : AC + BC ngắn nhất khi:
AC + BC = AB
=> C nằm giữa A và B
Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây dẫn ngắn nhất là C nằm giữa A và B

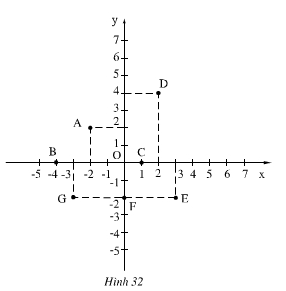
Tọa độ các điểm đó là:
A(-2; 2) ; B(-4; 0)
C(1; 0) ; D(2; 4)
E(3; -2) ; F(0; -2)
G(-3; -2)

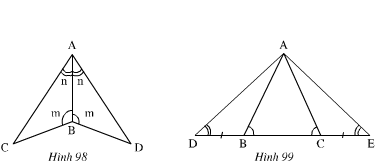
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)

Nếu nhân tuổi của ba chị em với nhau được 36, điều đó có nghĩa là tuổi của họ sẽ rơi vào một trong 8 trường hợp sau đây:
36 = 2 x 3 x 6, tổng số tuổi của ba chị em là 11.
36 = 2 x 2 x 9, tổng số tuổi của ba chị em là 13.
36 = 4 x 9 x 1, tổng số tuổi của ba chị em là 14.
36 = 4 x 3 x 3, tổng số tuổi của ba chị em là 10.
36 = 18 x 2 x 1, tổng số tuổi của ba chị em là 21.
36 = 12 x 3 x 1, tổng số tuổi của ba chị em là 16.
36 = 6 x 6 x1, tổng số tuổi của ba chị em là 13.
36 = 36 x 1 x 1, tổng số tuổi của ba chị em là 38.
Dựa theo dữ kiện đầu bài đưa ra là "Cộng tuổi của ba chị em với nhau được 13", ta sẽ có hai trường hợp thỏa mãn là 2 + 2 +9 và 6 + 6 + 1.
Đây chính là lúc dữ kiện "Chị lớn nhất có tóc màu vàng hoe" được cho là vô dụng vào lúc đầu lại phát huy được tác dụng. Dữ kiện này cho thấy sẽ chỉ có một người chị lớn tuổi hơn cả. Ở hai trường hợp nêu trên, ta thấy trường hợp 2 + 2 + 9 là một chị và hai em sinh đôi, trong khi, trường hợp 6 + 6 +1 là hai chị sinh đôi và một em.
Chỉ có trường hợp một là thỏa mãn được yêu cầu của đầu bài. Như vậy, câu trả lời của bài toán này sẽ là một người chị lớn có 9 tuổi và hai em gái sinh đôi có cùng 2 tuổi.






Theo định lý Pytago ta có:
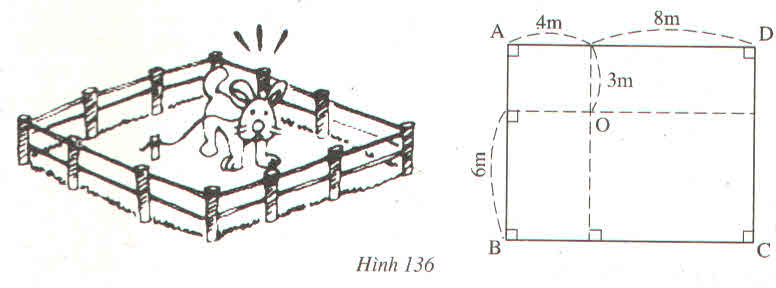
+) OA2 = 42 + 32 = 16 + 9 = 25
⇒ OA = 5m < 9m
+) OC2 = 62 + 82 = 36 + 64 = 100
⇒ OC = 10m > 9m
+) OB2 = 42 + 62 = 16 + 36 = 52
⇒ OB = √52m ≈ 7,21 (m) < 9m
+) OD2 = 32 + 82 = 9 + 64 = 73
⇒ OD = √73 ≈ 8,54(m) < 9m
Như vậy con Cún có thể tới các vị trí A, B, D nhưng không tới được vị trí C.