Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
\(f(x)>0\Leftrightarrow 2x-4>0\Leftrightarrow 2x>4\Leftrightarrow x>2\) hay \(x\in (2;+\infty)\)
Suy ra khẳng định $a$ đúng

a/ \(\left[{}\begin{matrix}\Delta>0\\\left\{{}\begin{matrix}\Delta\le0\\a>0\end{matrix}\right.\end{matrix}\right.\)
b/ \(\left[{}\begin{matrix}\Delta\ge0\\\left\{{}\begin{matrix}\Delta\le0\\a>0\end{matrix}\right.\end{matrix}\right.\)
c/ \(\left[{}\begin{matrix}\Delta\ge0\\\left\{{}\begin{matrix}a< 0\\\Delta\le0\end{matrix}\right.\end{matrix}\right.\)
d/ \(\left[{}\begin{matrix}\Delta\ge0\\\left\{{}\begin{matrix}a< 0\\\Delta\ge0\end{matrix}\right.\end{matrix}\right.\)

Lời giải:
\(f(x)=(-x+1)(x-2)>0\Leftrightarrow \left\{\begin{matrix} -x+1< 0\\ x-2< 0\end{matrix}\right.\) hay $1< x< 2$
hay $x\in (1;2)$
Đáp án D

a) f(-\(\dfrac{1}{2}\))= - \(\dfrac{1}{2}\)+1=\(\dfrac{1}{2}\)
f(0)=0+1=1
f(-1)=-1+1=0
b) f(x)=0 <=> x+1=0 <=>x=-1
f(x)=2 <=> x+1=2 <=>x=1
c) với điểm A(\(\dfrac{3}{4}\);\(\dfrac{-1}{2}\)) thay vào hàm số ta có -2*\(\dfrac{3}{4}\)+1=\(\dfrac{-1}{2}\)=\(\dfrac{-1}{2}\)
=> điểm A có thuộc đồ thị hàm số trên
làm tương tự vs các điểm còn lại nha bạn !

mk chỉ cho cách lm ; bn tự lm cho bt nha
câu a : lập bảng sét dấu tìm được \(x\) để \(y>0;y< 0\)
tiếp là đưa nó về dạng bình phương 1 số cộng 1 số \(\left(n^2+m\right)\) rồi tìm \(y_{min}\)
câu b : giao điểm của \(\left(P\right)\) và đường thẳng \(\left(d\right):y=2x+1\)
là nghiệm của hệ phương trình : \(\left\{{}\begin{matrix}y=x^2-2x-1\\y=2x+1\end{matrix}\right.\)

Câu 1: đáp án B, thay tọa độ A vào pt được \(1\le0\) (sai)
Câu 2: đáp án D
\(\left(m+n\right)^2\ge4mn\Leftrightarrow m^2+n^2+2mn\ge4mn\Leftrightarrow m^2+n^2\ge2mn\)
Câu 3: đáp án D
\(m=x^2+y^2\ge\frac{\left(x+y\right)^2}{2}=\frac{4}{2}=2\)
Câu 4:
\(\Leftrightarrow5x-\frac{2}{5}x>4\Leftrightarrow\frac{23}{5}x>4\Leftrightarrow x>\frac{20}{23}\)
Câu 5:
\(f\left(x\right)>0\Leftrightarrow23x-20>0\Leftrightarrow x>\frac{20}{23}\) đáp án C
Câu 6:
Bạn viết sai đề, nhìn BPT đầu tiên \(2x-5-1>0\) là thấy có vấn đề
Câu 7:
\(3x+2\left(y+3\right)>4\left(x+1\right)-y+3\)
\(\Leftrightarrow x-3y+1< 0\)
Thay tọa độ D vào ta được \(-1< 0\) đúng nên đáp án D đúng
Câu 8:
Thay tọa độ vào chỉ đáp án D thỏa mãn
Câu 9:
Đáp án C đúng
Câu 10:
Đáp án B đúng (do tọa độ x âm ko thỏa mãn BPT đầu tiên)

a, Bảng biến thiên:
Đồ thị hàm số:
b, \(f\left(x\right)>0\Leftrightarrow x\in\left(-\infty;-3\right)\cup\left(-1;+\infty\right)\)
\(f\left(x\right)< 0\Leftrightarrow x\in\left(-3;-1\right)\)
c, Yêu cầu bài toán là gì vậy:v
d, Phương trình hoành độ giao điểm của \(\left(P\right);\left(d\right)\):
\(x^2+4x+3=2x+m-5\)
\(\Leftrightarrow x^2+2x+8-m=0\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm phân biệt khi phương trình \(\left(1\right)\) có hai nghiệm phân biệt
\(\Delta'=1-\left(8-m\right)=m-7>0\Leftrightarrow m>7\)

a) Tập xác định của f(x) :
A = {x ∈ R | x2 + 3x + 4 ≥ 0 và -x2 + 8x – 15 ≥ 0}
- x2 + 3x + 4 có biệt thức Δ = 32 – 16 < 0
Theo định lí dấu của tam thức:
x2 + 3x + 4 ≥ 0 ∀x ∈R
-x2 + 8x – 15 = 0 ⇔ x1 = 3, x2 = 5
-x2 + 8x – 15 > 0 ⇔ 3 ≤ x ≤ 5 ⇒ A = [3, 5]
b) A/B = [3, 4]
R\(A\B) = (-∞, 3) ∪ (4, +∞)
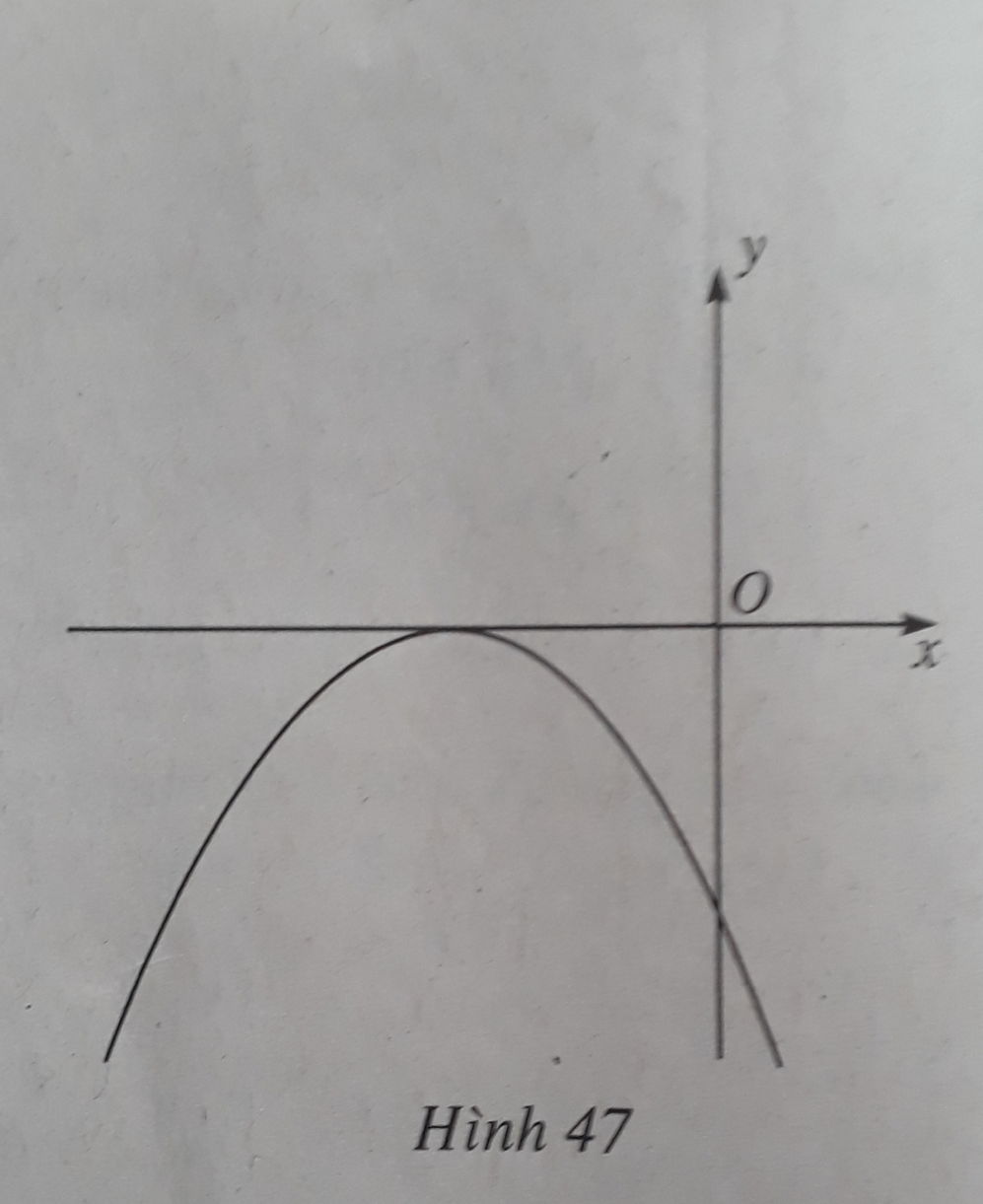
Đáp án: A