Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Pitago: \(BC^2=AB^2+AC^2\Rightarrow BC^2-\left(AB^2+AC^2\right)=0\)
Gọi các tiếp điểm với AB và AC là E và F
Do đường tròn (I) nội tiếp tam giác, theo t/c hai tiếp tuyến cắt nhau:
\(BD=BE\) ; \(AE=AF\) ; \(CD=CF\)
Mà \(BD+CD=BC;AE+BE=AB;AF+CF=AC\)
\(\Rightarrow BC+AB-AC=BD+CD+AB+BE-AF-CF=BD+BE=2BD\)
\(\Rightarrow BD=\dfrac{BC+AB-AC}{2}\)
Tương tự: \(BC+AC-AB=2DC\Rightarrow DC=\dfrac{BC+AC-AB}{2}\)
\(\Rightarrow BD.DC=\dfrac{1}{4}\left(BC+AB-AC\right)\left(BC+AC-AB\right)=\dfrac{1}{4}\left[BC^2-\left(AB-AC\right)^2\right]\)
\(=\dfrac{1}{4}\left(BC^2-\left(AB^2+AC^2\right)+2AB.AC\right)=\dfrac{1}{2}AB.AC=S_{ABC}\)

BÀI LÀM
a, xét tứ giác ADOE có:
góc A= góc E=góc D=90O
mà ta thấy: OE=OD( bán kính = nhau)
vậy tứ giác ADOE là hình vuông (dhnb)
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có SΔABC=SΔOAB+SΔOBC+SΔOAC
=12 OD.AB+12 OE.AC+12 OH.BC
=12 r.(AB+AC+BC)
=12 pr (pp là chu vi của tam giác ABCABC, rr là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: BC=√AB2+AC2=10(cm).
Diện tích tam giác ABC là: 12 AB.AC=12 .6.8=24(cm2).
Chu vi tam giác ABC là: 6+8+10=24(cm).
Suy ra: 24=12 .24.r⇔r=2(cm).

(Bởi vì CM trực tiếp hơi khó nên mình CM bằng trùng hình)
Vẽ \(AM\) là trung tuyến của tam giác \(ABC\) và tia \(AE\) thoả \(\widehat{BAE}=\widehat{CAM}\) (trong đó \(E\in\left(O\right)\)). Gọi \(D',N\) lần lượt là trung điểm của \(AE,AC\).
-----
Bước 1: CM: \(\widehat{AD'O}=90^o\) (hiển nhiên).
Bước 2: CM \(D\) trùng với \(D'\).
Tam giác \(ABE\) và \(AMC\) đồng dạng (g.g) nên tam giác phân bởi đường trung tuyến cũng đồng dạng.
Cụ thể là tam giác \(ABD'\) và \(AMN\) đồng dạng.
Suy ra \(\widehat{ABD'}=\widehat{AMN}=\widehat{BAM}\) (so le trong, \(MN\) song song \(AB\)).
Mà \(\widehat{BAM}=\widehat{EAC}\) nên \(\widehat{ABD'}=\widehat{D'AC}\).
Từ đó suy ra \(AC\) tiếp xúc với đường tròn ngoại tiếp \(ABD'\).
Tương tự suy ra \(AB\) tiếp xúc với đường tròn ngoại tiếp \(ACD'\).
Vậy \(D\) trùng với \(D'\) và ta có đpcm.

A B C N D F I K O
a) +) Ta có: IB, IK là 2 tiếp tuyến kẻ từ I
=> IO là tia phân giác \(\widehat{BIK}\)=->\(\widehat{BIO}=\frac{1}{2}\widehat{KIB}\)(1)
Tương tự: \(\widehat{IBO}=\frac{1}{2}\widehat{IBC}\)(2)
+) ND cùng vuông góc với IK và BC
=> IK//BC
=> \(\widehat{KIB}+\widehat{IBC}=180^o\)(3)
Từ (1), (2), (3)
=> \(\widehat{IBO}+\widehat{BIO}=90^o\)=> \(\widehat{IBO}=90^o\)
+) Xét 2 tam giác vuông INO và ODB có:
\(\widehat{ION}=\widehat{OBD}\)( cùng phụ với góc BOD)
=> \(\Delta INO~\Delta ODB\)
=> \(\frac{IN}{OD}=\frac{ON}{BD}\)=> \(IN.BD=R^2\)( với R là bán kính đường tròn (O)) (4)
Tương tự ta cũng chứng minh được: \(NK.DC=R^2\)(5)
(4), (5)=> \(IN.BD=NK.DC\Rightarrow\frac{IN}{NK}=\frac{DC}{BD}\)(6)
b) IK//BC. Theo định lí Thaslet ta có:
\(\frac{IN}{BE}=\frac{NK}{EC}\left(=\frac{AN}{AE}\right)\Rightarrow\frac{IN}{NK}=\frac{BE}{EC}\)(7)
(6),(7)=> \(\frac{DC}{DB}=\frac{BE}{EC}\Rightarrow\frac{BC-BD}{DB}=\frac{BC-EC}{CE}\Rightarrow\frac{BC}{BD}-1=\frac{BC}{CE}-1\Rightarrow\frac{BC}{BD}=\frac{BC}{CE}\Rightarrow BD=CE\)

A B D C I
Đặt BC = a , AC = b , AB = c . Ta có :
\(BD=\frac{a+c-d}{2}\)
\(DC=\frac{a+b-c}{2}\)
Do đó , ta giả sử \(\left(b\ge c\right)\)
\(BD.DC=\frac{a+c-b}{2}.\frac{a+b-c}{2}\)
\(=\frac{a-\left(b-c\right)}{2}.\frac{a+\left(b-c\right)}{2}\)
\(=\frac{a^2-\left(b-c\right)^2}{4}\)
\(=\frac{a^2-b^2+2bc-c^2}{4}\)
\(=\frac{a^2-\left(b^2+c^2\right)+2bc}{4}\)
Do \(a^2=b^2+c^2\)nên \(BD.DC=\frac{2bc}{3}=\frac{bc}{2}=S_{ABC}\)

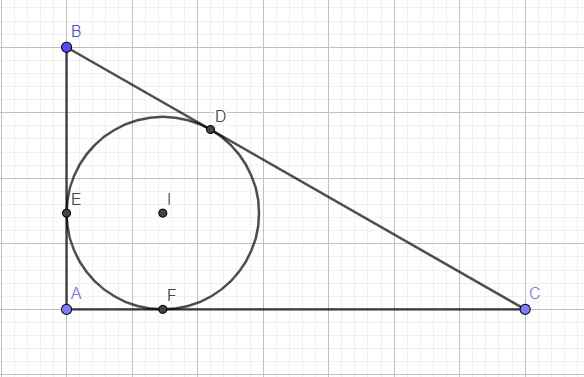
Gọi E và F lần lượt là tiếp điểm của đường tròn với AD và AC
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AE = AF
BE = BD
CD = CF
BD = BC + CD
BE = AB – AE
Suy ra: BD + BE = AB + BC – (AE + CD)
= AB + BC – (AE + CE)
= AB + BC – AC
Suy ra: BD = (AB + BC - AC)/2
Lại có: CD = BC – BD
CF = AC = AF
Suy ra: CD + CF = BC + AC – (BD + AF)
= BC + AC – (BE + AE)
= BC + AC – BA
Vậy S A B C = BD.DC.
sao k chụp ht bài luôn