Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A H B C D E 1 2
a) AB là đường trung trực của HD \(\Rightarrow\) AD = AH.
AC là đường trung trực của HE \(\Rightarrow\) AE = AH.
Suy ra AD = AE. (1)
Tam giác AHD cân nên \(\widehat{HAD}=2\widehat{A_1}.\)
Tam giác AHE cân nên \(\widehat{HAE}=2\widehat{A_2}.\)
Suy ra \(\widehat{HAD}+\widehat{HAE}=2\widehat{A_1}+2\widehat{A_2}=2\left(\widehat{A_1}+\widehat{A_2}\right)\)
\(\widehat{HAD}+\widehat{HAE}=2.90^o=180^o.\)
Do đó D, A, E thẳng hàng. (2)
Từ (1) và (2) suy ra A là trung điểm của DE. Vậy D đối xứng với E qua A.
b) Tam giác DHE có HA là đường trung tuyến và HA = \(\dfrac{1}{2}\) DE nên \(\Delta DHE\) vuông tại H.
c) Hãy chứng minh \(\widehat{ADB}=\widehat{AHB}=90^o,\widehat{AEC}=90^o\) để suy ra BDEC là hình thang vuông
d) Hãy chứng minh BD = BH, CE = CH.

a: Vì H và D đối xứng nhau qua AB
nên AH=AD; BH=BD
Xét ΔAHB và ΔADB có
AH=AD
HB=DB
AB chung
Do đó ΔAHB=ΔADB
Suy ra: góc ADB=90 độ và góc HAB=góc DAB
hay BD vuông góc với AD và AB là phân giác của góc HAD(1)
b: Ta có: H và E đối xứng nhau qua AC
nên AH=AE; CH=CE
=>ΔAHC=ΔAEC
=>góc AEC=90 độ và góc HAC=góc EAC
=>AC là phân giác của góc HAE(2)
Ta có: CH+BH=BC
=>BD+CE=BC
c: Từ (1) và (2) suy ra góc DAE=2x90=180 độ
=>D,A,E thẳng hàng

a) Vì D là điềm đối xứng với H qua AB nên AB là đường trung trực của DH
suy ra AH=AD (1)
Vì E đối xứng với H qua AC nên AC là đường trung trực của HE
suy ra AH=AE (2)
Từ (1) và (2) suy ra AD=AE (3)
Mặt khác ^DAB=^BAH; ^HAC=^CAE và ^BAH+^HAC=90*
do đó ^DAB+^BAH+ ^HAC+^CAE=180*
tức là D, A, E thẳng hàng (4)
từ (3) và (4) suy ra D và E đối xứng với nhau qua A.
b) Tam giác DHE có HA là trung tuyến và HA= 1/2 DE
nên tam giác DHE vuông tại H.
c) Tam giác ADB=tam giác AHB (c-c-c)
suy ra ^ADB=^AHB=90*
tương tự có ^AEC=90*
suy ra BD//CE (cùng vuông góc với DE)
nên tứ giác BAEC là hình thang có 2 góc vuông kề cạnh bên DE
nên BAEC là hình thang vuông.
d) Do AB là đường trung trực của DH nên BD=BH (5)
Do AC là đường trung trực của EH nên CE=CH (6)
công vế với vế của (5) và (6) ta có BD+CE=BH+CH
hay BD+CE=BC
đó nha bn

a) Vì D là điềm đối xứng với H qua AB nên AB là đường trung trực của DH
\(\Rightarrow\) AH=AD (1)
Vì E đối xứng với H qua AC nên AC là đường trung trực của HE
\(\Rightarrow\) AH=AE (2)
Từ (1) và (2) \(\Rightarrow\) AD=AE (3)
Mặt khác \(\widehat{DAB}=\widehat{BAH}\); \(\widehat{HAC}=\widehat{CAE}\) và \(\widehat{BAH}+\widehat{HAC}=90^0\)
Do đó \(\widehat{DAB}+\widehat{BAH}+\widehat{HAC}+\widehat{CAE}=180^0\)
Tức là D, A, E thẳng hàng (4)
Từ (3) và (4) \(\Rightarrow\) D và E đối xứng với nhau qua A.
b) Tam giác DHE có HA là trung tuyến và HA= \(\frac{1}{2}\) DE
Nên tam giác DHE vuông tại H.
c) Tam giác ADB = tam giác AHB ( có chung chiều cao )
\(\Rightarrow\widehat{ADB}=\widehat{ABH}=90^0\)
Tương tự có \(\widehat{AEC}=90^0\)
\(\Rightarrow\) BD//CE (cùng vuông góc với DE)
Nên tứ giác BAEC là hình thang có 2 góc vuông kề cạnh bên DE
Nên BAEC là hình thang vuông.
d) Do AB là đường trung trực của DH nên BD=BH (5)
Do AC là đường trung trực của EH nên CE=CH (6)
Cộng vế với vế của (5) và (6) ta có BD+CE=BH+CH
Hay BD+CE=BC

1a/IM vuông góc AB=>AMI=90 do
IN vuông góc AC=>ANI=90 do
△ABC vuông tại A=>BAC=90 do
=>góc AMI= gocANI= gocBAC= 90 do => tứ giác AMIN là hình chữ nhật
1b/Có I dx vs D qua N => ID là đường trung trực của AC=>AI=AD; IC=ID(1)
Trong △ABC có AI là đường trung tuyến ứng với cạnh huyền BC =>AI=1/2BC hay AI=IC(2)
Từ (1) va (2) => AI=IC=CD=DA => Tu giac AICD la hthoi
2a/ Có M là TĐ AB và M là điểm đối xứng giữa E và H
=> AM=MB VA EM=MH hay AB giao voi EH tai TD M
=> Tg AEBH la hbh co AHB=90 do => Hbh AEBH la hcn
2b/Co AEBH la hcn=>EH=AB
+) Mà AB=AC=>EH=AC(1)
+) △ABC cân tại A có AH là đường cao đồng thời phân giác của góc BAC => góc BAH=góc HAC.
Co goc BAH=1/2 EAH ; góc AHE=1/2AHB
Ma goc EAH= goc AHB=>BAH=AHE hay goc HAC= goc AHE.
Mà 2 góc này ở vị trí SLT=> EH//AC(2)
Từ (1) va (2)=>tg AEHC la hbh

a) Vì D là điềm đối xứng với H qua AB nên AB là đường trung trực của DH
=> AH=AD (1)
Vì E đối xứng với H qua AC nên AC là đường trung trực của HE
=> AH=AE (2)
Từ (1) và (2) suy ra AD=AE (3)
Mặt khác góc DAB=gócBAH; gócHAC= góc CAE và góc BAH+góc HAC=90o
do đó góc DAB+góc BAH+góc HAC+góc CAE=180o
=> D, A, E thẳng hàng (4)
từ (3) và (4) suy ra D và E đx với nhau qua A.
b) Tam giác DHE có HA là trung tuyến và HA= 1/2 DE
=> tam giác DHE vuông tại H.
c) Tam giác ADB=tam giác AHB (c-c-c)
suy ra góc ADB=góc AHB=90o
tương tự ta có : góc AEC=90o
suy ra BD//CE (cùng vuông góc với DE)
nên tứ giác BAEC là hình thang có 2 góc vuông kề cạnh bên DE
=> BAEC là hình thang vuông.
a) Vì D là điểm đối xứng với H qua AB nên AB là đường trung trực của DH
=> AH=AD (1)
Vì E đối xứng với H qua AC nên AC là đường trung trực của HE
=> AH=AE (2)
Từ (1) và (2) suy ra AD=AE (3)
Mặt khác góc DAB= góc BAH; góc HAC=góc CAE và góc BAH+góc HAC=90o
Do đó góc DAB + góc BAH+ góc HAC + góc CAE=180o
=> D, A, E thẳng hàng (4)
Từ (3) và (4) suy ra D và E đx với nhau qua A.
b) Tam giác DHE có HA là trung tuyến và HA= 1/2 DE
=> tam giác DHE vuông tại H.
c) Tam giác ADB=tam giác AHB (c-c-c)
suy ra góc ADB=góc AHB=90o
tương tự ta có góc AEC=90o
=> BD//CE (cùng vuông góc với DE)
nên tứ giác BDEC là hình thang có 2 góc vuông kề cạnh bên DE
=> BDEC là hình thang vuông.

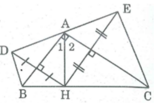
Điểm D đối xứng điểm H qua trục AB.
Suy ra AB là đường trung trực của HD
⇒ AH = AD (tính chất đường trung trực)
⇒ ∆ ADH cân tại A
Suy ra: AB là tia phân giác của ∠ (DAH)
⇒ ∠ (DAB) = ∠ A 1
Điểm H và điểm E đối xứng qua trục AC
⇒ AC là đường trung trực của HE
⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A
Suy ra: AC là đường phân giác của góc (HAE) ⇒ ∠ A 2 = ∠ (EAC)
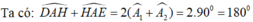
⇒ D, A, E thẳng hàng
Ta có: AD = AE (vì cùng bằng AH)
Suy ra điểm A là trung điểm của đoạn DE.
Vậy điểm D đối xứng với điểm E qua điểm A
∆ ADB = ∆ AHB ⇒ BD = BH.
∆ AEC = ∆ AHC ⇒ CE = CH.
Vậy BD + CE = BH + CH = BC.