Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

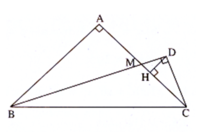
Theo câu a), từ AB = 2AM, suy ra HC = 2HD. Ta có HC < MC (h là chân đường cao hạ từ D của tam giác DCM vuông tại D) nên HC = 2HD < MC = AM < AH (do M nằm giữa A và H), vì thế 2HD không thể bằng AH. Khẳng định b) là sai.

a: Xét ΔHCD vuông tại H và ΔABM vuông tại A có
góc HCD=góc ABM
Do đó: ΔHCD đồng dạng với ΔABM
b: Khẳng định này sai

. A B O H C d
a) VÌ: \(OC\perp EF\left(gt\right)\)
\(AE\perp EF\left(gt\right)\)
=> OC//AE
=> \(\widehat{EAC}=\widehat{OCA}\) ( cặp góc sole trong) (1)
Vì: OC=OA(gt)
=> ΔOAC cân tại O
=> \(\widehat{OCA}=\widehat{OAC}\) (2)
Từ (1);(2) suy ra:
\(\widehat{EAC}=\widehat{OAC}\)
=>AC là tia pg của \(\widehat{BAE}\)
b)Chứng minh tương tự như câu a ta có: \(\widehat{OBC}=\widehat{FBC}\)
Xét ΔAEC và ΔAHC có:
\(\widehat{AEC}=\widehat{AHC}=90^o\)
AC:cạnh chung
\(\widehat{EAC}=\widehat{HAC}\left(cmt\right)\)
=>ΔAEC=ΔAHC ( cạnh huyền -góc nhọn)
=>AE=AH
Xét ΔCHB và ΔCFB có:
\(\widehat{CHB}=\widehat{CFB}=90^o\)
BC:cạnh chung
\(\widehat{HBC}=\widehat{FBC}\left(cmt\right)\)
=> ΔCHB=ΔCFB(ch-gn)
=> BF=HB
Xét ΔABC có: OA=OB=OC
=> ΔABC cân tại C
=> \(CH^2=AH\cdot BH\)
Hay: \(CH^2=AE\cdot BF\)

Dễ mà!
Câu a): \(\widehat{ECA}=\widehat{CBH}=\widehat{ACH}\) nên \(\widehat{EAC}=\widehat{HAC}\).
Câu b): Từ câu a) CM được tam giác \(ECA\) và \(HCA\) là bằng nhau, tức là \(EA=HA\)
Tương tự, \(FB=HB\) nên \(BF.AE=AH.BH=CH^2\)

d A O H B C
a ) Vì \(OC\perp EF\left(gt\right)\)
\(AE\perp EF\left(gt\right)\)
\(\Rightarrow OC//AE\)
\(\Rightarrow\widehat{EAC}=\widehat{OCA}\) ( cặp góc so le trong ) (1)
Vì : OC = OA ( gt)
\(\Rightarrow\Delta OAC\) cận tại O
\(\Rightarrow\widehat{OCA}=\widehat{OAC}\left(2\right)\)
Từ (1) và (2) suy ra :
\(\widehat{EAC}=\widehat{OAC}\)
\(\Rightarrow\) AC là tia phân giác của \(\widehat{BAE}\)
b ) Chứng minh tương tự như câu a ta có :
\(\widehat{OBC}=\widehat{FBC}\)
Xét \(\Delta AEC\) và \(\Delta AHC\) có :
\(\widehat{AEC}=\widehat{AHC}=90^o\)
AC : cạnh chung
\(\widehat{EAC}=\widehat{HAC}\left(cmt\right)\)
\(\Rightarrow\Delta AEC=\Delta AHC\) ( cạnh huyền - góc nhọn )
\(\Rightarrow AE=AH\)
Xét \(\Delta CHB\) và \(\Delta CFB\) có :
\(\widehat{CHB}=\widehat{CFB}=90^o\)
BC : cạnh chung
\(\widehat{HBC}=\widehat{FBC}\left(cmt\right)\)
\(\Rightarrow\Delta CHB=\Delta CFB\left(ch-gn\right)\)
\(\Rightarrow BF=HB\)
Xét : tam giác ABC có : OA = OB =OC
\(\Rightarrow\Delta ABC\) cân tại C
\(\Rightarrow CH^2=AH.BH\)
Hay \(CH^2=AE.BF\)
Chúc bạn học tốt !!!


Hai tam giác vuông HCD và DCM đồng dạng (có cùng góc nhọn tại C) mà
∆ DCM ∼ ∆ ABM (vì là hai tam giác vuông có ∠ (DMC) = ∠ (AMB), vậy ∆ HCD ∼ ∆ ABM. Khẳng định a) là đúng.