Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AB = AC (gt)
=> Tam giác ABC cân tại A
Xét tam giác EAB và tam giác DAC có:
EA = DA (gt)
A chung
AB = AC (gt)
=> Tam giác EAB = Tam giác DAC (c.g.c)
=> EB = DC (2 cạnh tương ứng)
EBA = DCA (2 góc tương ứng)
mà ABC = ACB (tam giác ABC cân tại A)
=> ABC - EBA = ACB - DCA
hay EBC = DCB
=> Tam giác OBC cân tại O
Xét tam giác BOD và tam giác COE có:
DBO = ECO (tam giác EAB = tam giác DAC)
BO = CO (tam giác OBC cân tại O)
BOD = COE (2 góc đối đỉnh)
=> Tam giác BOD = Tam giác COE (c.g.c)

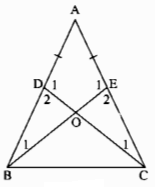
a) Xét ∆BEA và ∆CDA, ta có:
BA = CA (gt)
\(\widehat{A}\)chung
AE = AD (gt)
Suy ra: ∆BEA = ∆CDA (c.g.c)
Vậy BE = CD (hai cạnh tương ứng)
b) ∆BEA = ∆CDA (chứng minh trên)
⇒\(\widehat{\text{B1}}=\widehat{\text{C1}}\);\(\widehat{\text{E1}}=\widehat{\text{D1}}\) (hai góc tương ứng)
\(\widehat{\text{E1}}+\widehat{\text{E2}}\)=180o (hai góc kề bù)
\(\widehat{\text{D1}}+\widehat{\text{D2}}\)=180o (hai góc kề bù)
Suy ra: \(\widehat{\text{E2}}=\widehat{\text{D2}}\)
AB = AC (gt)
⇒ AE + EC = AD + DB mà AE = AD (gt) => EC = DB
Xét ∆ODB và ∆OCE, ta có:
\(\widehat{\text{E2}}=\widehat{\text{D2}}\) (chứng minh trên)
DB = EC (chứng minh trên)
\(\widehat{\text{B1}}=\widehat{\text{C1}}\)(chứng minh trên)
Suy ra: ∆ODB = ∆OEC (g.c.g)

Bài 2:
Xét ΔADO vuông tại D và ΔAEO vuông tại E có
AO chung
\(\widehat{DAO}=\widehat{EAO}\)
Do đó: ΔADO=ΔAEO
Suy ra: OD=OE
Bài 3:
Xét ΔABE và ΔACD có
AB=AC
\(\widehat{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD

Bài giải
A B C D E K
a, Xét \(\Delta AEB\) và \(\Delta ADC\) , có :
\(AD=AE\) ( giả thiết )
\(\widehat{A}\) : góc chung
\(AB=AC\) ( giả thiết )
\(\Rightarrow\text{ }\Delta AEB=\Delta ADC\) \(\left(c\text{ - }g\text{ - }c\right)\)
\(\Rightarrow\text{ }BE=CD\text{ ( cạnh tương ứng )}\)
b, AB = AC , AD = AE => AB - AD = AC - AE hay DB = EC
Xét \(\Delta BCD\)và \(\Delta CBE\)có:
BC : cạnh chung
CD = BE ( chứng minh trên )
BD = CE ( chứng minh trên )
\(\Rightarrow\text{ }\Delta BCD=\Delta CBE\text{ }\left(c\text{ - }c\text{ - }c\right)\)
\(\Rightarrow\text{ }\widehat{ BDC}=\widehat{\text{ CEB}}\)( hai góc tương ứng )
Xét \(\Delta KBD\) và \(\Delta KCE\)có:
\(\widehat{BDC}=\widehat{CEB}\)( chứng minh trên )
BD = CE ( chứng minh trên )
\(\widehat{ABK}=\widehat{ACK}\) ( 2 góc tương ứng do \(\Delta ABE=\Delta ACD\) )
\(\Rightarrow\text{ }\Delta KBD=\Delta KCE\left(g\text{ - }c\text{ - }g\right)\)

Nguyễn Thuỳ Linh Hình như bài này t lm cho c r mà nhỉ
( Hình tự vẽ )
a) +) Xét \(\Delta\)ABE và \(\Delta\)ACD có
AB = AC ( gt)
\(\widehat{BAC}\) : góc chung
AE = AD ( gt)
=> \(\Delta\)ABE = \(\Delta\)ACD (c-g-c)
b) Theo câu a ta có \(\Delta\)ABE = \(\Delta\)ACD
=> BE = CD ( 2 cạnh tương ứng )
c) +) Xét \(\Delta\) ABC cân tại A
=> \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\) (1) ( tính chất tam giác cân )
+) Xét \(\Delta\)AED có AE = AD ( gt)
=> \(\Delta\)AED cân tại A
=> \(\widehat{AED}=\frac{180^o-\widehat{A}}{2}\) (2) ( tính chất tam giác cân )
Từ (1) và (2) \(\Rightarrow\widehat{ABC}=\widehat{AED}\)
Mà 2 góc này ở vị trí đồng vị
=> ED // BC
@@ Hc tốt
Takigawa Miu_

a/ Xét 2 tam giác BDE và CED có
BD=EC
DE chung
Góc BDE = góc DEC do chúng lần lượt bù với 2 góc bằng nhau là ADE và AED
=> dpcm (c.g.c)
b/ Có góc DKB bằng góc EKC do đối đỉnh
KD=KE
góc BDK=góc CEK
Vậy tam giác BOD = tam giác COE
Xét ΔBEA và CDA, ta có:
BA = CA (giả thiết)
∠A chung
AE=AD (giả thiết)
Suy ra: ΔBEA = ΔCDA (c.g.c)
Vậy: BE = CD (hai cạnh tương ứng)