Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}=53^0\)
=>\(\widehat{C}=37^0\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=4,8(cm)
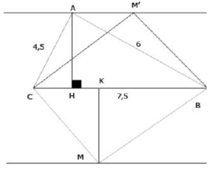
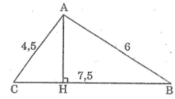
a. Ta có: AB2 = 62 = 36
AC2 = 4,52 = 20,25
BC2 = 7,52 = 56,25
Vì AB2 + AC2 = 36 + 20,25 = 56,25 = BC2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
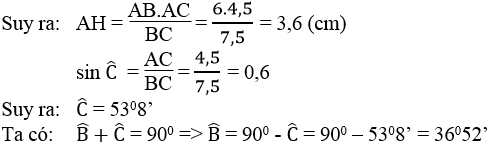b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
a) Ta có: A B 2 + A C 2 = 6 2 + 4 , 5 2 = 7 , 5 2 = B C 2
nên tam giác ABC vuông tại A. (đpcm)
= > ∠ B = 37 ° = > ∠ C = 90 ° - ∠ B = 90 ° - 37 ° = 53 °
Mặt khác trong tam giác ABC vuông tại A, ta có:
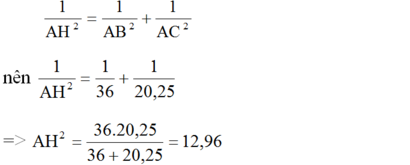
=> AH = 3,6 cm
b) Gọi khoảng cách từ M đến BC là MK. Ta có:
Ta thấy SMBC = SABC khi MK = AH = 3,6 cm
Do đó để SMBC = SABC thì M phải nằm trên đường thẳng song song và cách BC một khoảng là 3,6 cm (có hai đường thẳng như trên hình).
Cậu tự vẽ hình nhé
a, kẻ MK vuông BC, NG vuông BC
Tam g ABC cân => g ABC= g ACB
Lại có g ACB = g GCN (dd)
=> g GCN = g ABC=g MBK
Xét tg MBK và tg NCG
g MKB= g NGC =90°
g MBK = g NCG (cmt)
MB= CN(gt)
=> tg MBK= tg NCG ( ch-gn)
=> MK=NG (2 cạnh tương ứng)
Vì MK vuông BC, NG vuông BC => NG// MK
=> g GNM = g KMN ( so le trong )
Xét tg MKD VÀ TG NGD
g MKD = g DGN = 90°
g KMD = gDNG ( cmt)
Mk= GN (cmt)
=> tg MKD = tg NGD (_cgv-gn)
=> MD= ND (2 ctu)
=> D là td MN ( dpcm)
Xét tam giác cân ABC , AH là đường cao => AH là trung trực
Lại có E thuộc AH => EC= EB
Xét tg ABE và tg ACE
AB=AC (tg ABC cân)
BE= EC (cmt)
AE cạnh chung
=> tg ABE = tg ACE (ccc)
=> g ABE = g ACE ( 2 góc tương ứng)(1)
Lại có DE là trung trực MN => ME = NE
Xét tg MBE và tg NCE
MB = NC ( gt)
ME = NE (cmt)
BE = CE (cmt)
=> tg MBE = tg NCE (ccc)
=> g ECN = g EBM (2 góc t u ) (2)
Từ 1), 2) => g ECA = g ECN
Lại có 2 góc này bù nhau
=>g ACE= 90°= g ABE
Xét tg ABE vuông
+ theo đl pytago:
=> AE = √( ab2+bE2)= √( 62+4,52)= 7,5 (cmcm)
+ BH là đcao, theo hệ thức lượng trong tg vuông
=>+ AB2= AH.AE => AH= 62:7,5=4,8 (cmcm)
+ 1/(BH2)= 1/(AB2)+1/(BE2) => BH = √(1:( (1/62)+(1/4,52))= 3,6(ccmcm)
=> BC= 3,6.2= 7,2 (cm)
=> dt tg ABC có đcao AH là 7,2.4,8.1/2= 28,08(cm2)
Vậy S tg ABC = 28,08 cm2
a)ta thấy AB^2+AC^2=56.25 và BC^2=56.25
=>AB^2+BC^2=BC^2<=>tam jác ABC vuông tại A
Sin B=AC/BC=4.5/7.5<=>B=36độ 52 phút 11.63 giây (bấm shift sin 4.5/7.5 =)
sin c=AB/BC =>C=53đô 7 phút 48.37 giây
Sin C=AH/Ac =>AH=sin C*AC=3.6
b)qua A kẻ đường thẳng d song song BC.diện tích tam jác ABC luôn bằng diện tích tam jác BMC khi M thuộc d.(vì MH sẽ luôn = AH
Ta có:
A B 2 = 6 2 = 36 A C 2 = 4 , 52 = 20 , 25 B C 2 = 7 , 52 = 56 , 25
Vì A B 2 + A C 2 = 36 + 20,25 = 56,25 = B C 2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
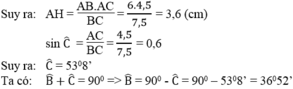
B C A M D F E
a) Ta có: \(S_{\Delta ABC}=S_{\Delta MBC}+S_{\Delta MCA}+S_{\Delta MAB}\)
\(\Rightarrow S_{\Delta ABC}=\frac{1}{2}MD.BC+\frac{1}{2}ME.AC+\frac{1}{2}MF.AB\)
\(\Rightarrow S_{\Delta ABC}=\frac{1}{2}ax+\frac{1}{2}by+\frac{1}{2}cz\)
\(\Rightarrow S_{\Delta ABC}=\frac{1}{2}\left(ax+by+cz\right)\)
\(\Rightarrow S=\frac{1}{2}\left(ax+by+cz\right)\)
\(\Rightarrow2S=ax+by+cz\)
=> đpcm
b) Ta có: \(\left(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\right)\left(ax+by+cz\right)=\left(a^2+b^2+c^2\right)+\left(\frac{a}{x}.by+\frac{b}{y}.ax\right)\) \(+\left(by.\frac{c}{z}+cz.\frac{b}{y}\right)+\left(cz.\frac{a}{x}+ax.\frac{c}{z}\right)\)
\(=\left(a^2+b^2+c^2\right)+ab\left(\frac{y}{x}+\frac{x}{y}\right)+bc\left(\frac{y}{z}+\frac{z}{y}\right)+ca\left(\frac{z}{x}+\frac{x}{z}\right)\)
\(\ge a^2+b^2+c^2+2ab+2by+2ca=\left(a+b+c\right)^2\)
(vì ta dễ chứng minh được \(\frac{x}{y}+\frac{y}{x}\ge2\) - tương tự với \(\frac{y}{z}+\frac{z}{y};\frac{z}{x}+\frac{x}{z}\))
Vậy \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\ge\frac{\left(a+b+c\right)^2}{\left(ax+by+cz\right)}=\frac{\left(a+b+c\right)^2}{2S}\)
Dấu "=" xảy ra <=> x = y = z
Vậy \(min\left(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\right)=\frac{\left(a+b+c\right)^2}{2S}\)
Hình bạn tự vẽ nha :v
a, áp dụng định lý pytago vào tam giác ABC có góc BAC =90 ta đc : BC2=AC2+AB2 thay vào là đc nha
áp dụng hệ thức lượng vào tam giác ABC có góc BAC=90 ta dc :AH.BC=AB.AC thay vào là đc nha
Mà AM=1/2 BC thay vào nha :v
b, Xét tam giác ABE và tam giác ABF có : góc ABF - góc chung và góc AEB= góc BAF=90 => tam giác ABE đồng dạng tam giác FBA => BE/BA=AB/FB=> BE.FB=AB2(1)
áp dụng hệ thức lượng vào tam giác ABC có góc BAC=90 ta đc : AB2 =BH.BC(2)
từ (1) và (2) => dpcm
Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời S A B C = S B M C nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.