Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : ADCT : \(I_0=U_0\sqrt{\frac{C}{L}}\) ( Từ công thức tính năng lượng điện từ trong mạch \(W=W_{Cmax}=W_{Lmax}\)
Nghĩa là :\(\frac{L.\left(I_0\right)^2}{2}=\frac{C.\left(U_0\right)^2}{2}\))
\(\Rightarrow I_0=5.\sqrt{\frac{8.10^{-9}}{2.10^{-4}}}=\text{0.0316227766}\left(A\right)\)\(\Rightarrow I=\frac{I_0}{\sqrt{2}}=\text{0.022360677977}\left(A\right)\)
Mà \(P=r.I^2\Rightarrow r=\frac{6.10^{-3}}{5.10^{-4}}=12\left(\Omega\right)\Rightarrow D\)

Bạn tham khảo hai bài tương tự này nhé:
Câu hỏi của Nguyễn Khánh Quỳnh - Học và thi online với HOC24
Câu hỏi của Hue Le - Học và thi online với HOC24

Ta có: \(\frac{hc}{\lambda}=A+\frac{1}{2}mv^2_{0max}\left(\text{∗}\right)\)
+Khi chiếu bức xạ có \(\lambda_1:v_{0max1}=\sqrt{\frac{2\left(\frac{hc}{\lambda_1}-A\right)}{m}}\left(1\right)\)
+Khi chiếu bức xạ có \(\lambda_2:v_{0max2}=\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}\left(2\right)\)
Từ \(\text{(∗)}\) ta thấy lhi \(\lambda\) lớn thì \(v_{0max}\) nhỏ
\(\Rightarrow v_{0max1}=2,5v_{0max2}\left(\lambda_1<\lambda_2\right)\)
\(\Leftrightarrow\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}=2,5\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}\)
\(\Leftrightarrow\frac{hc}{\lambda_1}-A=6,25\left(\frac{hc}{\lambda_2}-A\right)\) với \(A=\frac{hc}{\lambda_0}\)
\(\Rightarrow\lambda_0=\frac{5,25\lambda_1\lambda_2}{6,25\lambda_1-\lambda_2}=\frac{5,25.0,4.0,6}{6,25.0,4-0.6}=0,663\mu m\)

Quan sát và phân tích hiện tượng nước chảy ở ống nhỏ giọt ta thấy: đầu tiên giọt nước to dần nhưng chưa rơi xuống, đó là vì có các lực căng bề mặt tác dụng lên đường biên \(BB'\) của giọt nước, các lực này có xu hướng kéo co mặt ngoài của giọt nước lại, vì thế hợp lực của chúng hướng lên trên và có độ lớn \(\text{F=σl}\), với \(\text{l=πd}\),( \(d\) là đường kính miệng).
Đúng lúc giọt nước tách ra và rơi xuống thì trọng lượng \(P\) của giọt nước bằng lực căng bề mặt \(F\);
\(F=P\),
suy ra :
\(\text{σπd=mg}\) hay \(\sigma=\frac{mg}{\pi d}\left(1\right)\)
với \(m\) là khối lượng của \(1\) giọt nước. Theo đề bài \(2cm^3\) chứa \(200\) giọt nước, khối lượng \(2cm^3\) bằng \(2g\); vì vậy khối lượng của một giọt nước bằng
\(m=\frac{2g}{200}=0,01g=10^{-5}kg\)
Thay số vào (1) ta được: \(\sigma=\frac{9,8.10^{-5}}{3,14.0,4.10^{-3}}\approx0,078N\text{/}m\)
Hệ số căng bề mặt của nước bằng \(0,078N\text{/}m\)

1) Công thoát của êlectron ra khỏi bề mặt catôt
\(A=\frac{hc}{\lambda_0}=3,025.10^{-19}J\)
2) Vận tốc ban cực đại của electron
\(V_{max}=\sqrt{\frac{2hc}{m}\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)}=5,6.10^5m\text{/}s\)
3) Hiệu điện thế hãm để không có electron về catôt.
\(v_h=\frac{hc}{e}\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)=0,91V\)

2 trường hợp cho cùng cường độ dòng nên kháng trong 2 trường hợp như nhau và ta đã biết quận không thuần cảm
\(\frac{1}{C\omega_1}-L\omega_1=L\omega_2-\frac{1}{C\omega_1}\)
\(LC\omega_1\omega_2=1\)
\(Z_{C_1}=\frac{1}{C\omega_1}=L\omega_2=Z_{L_2}=62,5\Omega\)
\(Z_{L_1}=40\Omega\)
\(Z=\frac{U}{I}\approx54,83\Omega\)
\(r=50\Omega\)
Cường độ dòng hiệu dụng cực đại sẽ là
\(I'=\frac{U}{r}=4A\)
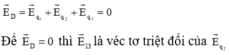
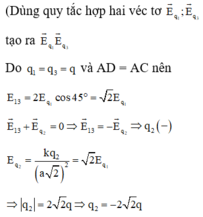
Đáp án D