Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
b) Câu b đou

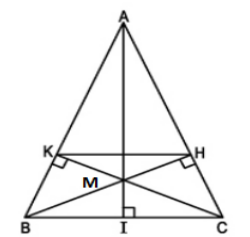
a)Ta có E là trung điểm của CM (gt)
F là trung điểm của CB (gt)
\(\Rightarrow\) EF là đường trung bình của (định nghĩa đường trung bình của tam giác)
\(\Rightarrow\) EF//MB (tính chất đường trung bình của tam giác)
hay EF//AB
lại có K là trung điểm của AD (gt)
F là trung điểm của CB (gt)
\(\Rightarrow\) KF là đường trung bình của (...)
\(\Rightarrow\) KF//AM (t/c ...)
hay KF//AB
nên EF//KF (vì cùng // với AB)
\(\Rightarrow\) tứ giác EFFIK là hình thang (Định nghĩa hình thang)
Gọi N là trung điểm của AM, nối KM
Ta có N là trung điểm của AM (cách dựng)
K là trung điểm của AD (gt)
\(\Rightarrow\) NK là đường trung bình của
nên NK//DM (t/c....)
mà EN là đường trung bình của (E,I là trung điểm của MC,AM)
\(\Rightarrow\) EI//AC (t/c...)
lại có và
là những tam giác đều (gt)
\(\Rightarrow\)
\(\Rightarrow\) AC//DM
tức là NK//EN (cùng //AC//DM)
do đó 3 điểm E,K,N thẳng hàng (theo tiên đề Ơ-clit)
(2góc đồng vị của AC//EN)
(2 góc đồng vị của KF//AM)
nên
C/m tương tự, lấy P là trung điểm của BM ta cũng được
Hình thang EFIK có
Vậy EFIK là hình thang cân (dấu hiệu nhận biết)
b) Ta có EFIK là hình thang cân (kq câu a)
\Rightarrow EI=KF (tính chất 2 đường chéo trong hình thang cân)
E là trung điểm của CM, I là trung điểm của DM (gt)
\(\Rightarrow\) EI là đường trung bình của tam giác CMD
\(\Rightarrow\) EI=
Vậy KF=

a: Xét ΔAHB vuông tại H và ΔDAB vuông tại A có
góc ABH chung
=>ΔAHB đồng dạng vơi ΔDAB
b: \(BD=\sqrt{12^2+16^2}=20\left(cm\right)\)
BH=12^2/20=7,2cm
AH=12*16/20=9,6cm

Vì
△
AHB đồng dạng
△
BCD với tỉ số đồng dạng: 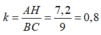
Ta có:  =
k
2
=
0
,
8
2
= 0,64 ⇒
S
A
H
B
=
0
,
64
.
S
B
C
D
=
k
2
=
0
,
8
2
= 0,64 ⇒
S
A
H
B
=
0
,
64
.
S
B
C
D
S B C D = 1/2 BC.CD = 1/2 .12.9 = 54( c m 2 )
Vậy S A H B = 0 , 64 . S B C D = 0,64.54 = 34,56 ( c m 2 ).

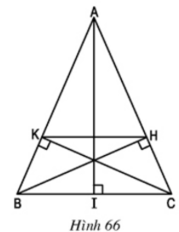
A B C K H I
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)

a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
góc ABH=góc BDC
=>ΔAHB đồng dạng với ΔBCD
b: BD=căn 9^2+12^2=15cm
AH=9*12/15=108/15=7,2cm
c: Xét ΔHAD có HN/HA=HP/HD
nên NP//AD và NP=AD/2
=>NP//BC và NP=BC/2
=>NP//BM và NP=BM
=>BNPM là hình bình hành
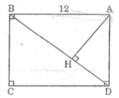

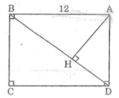
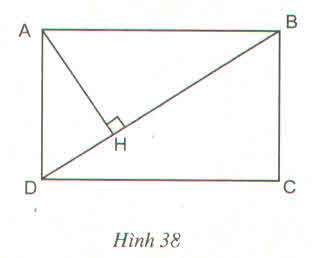


Vì △ AHB đồng dạng △ BCD nên:
Suy ra: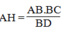
Áp dụng định lí Pi-ta-go vào tam giác vuông BCD,ta có:
B D 2 = B C 2 + C D 2 = B C 2 + A B 2
= 12 2 + 9 2 = 225
Suy ra: BD = 15cm
Vậy AH = (12.9)/15 = 7,2 cm