Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi I' là ảnh của I qua phép biến hình nói trên
a) Phương trình của đường tròn (I;3) là ( +
= 9
b) (I) = I' (1;-1), phương trình đường tròn ảnh :
c) (I) = I'(3;2), phương trình đường tròn ảnh:
d) (I) = I'( -3;2), phương trình đường tròn ảnh:
Gọi I' là ảnh của I qua phép biến hình nói trên
a) Phương trình của đường tròn (I;3) là ( +
= 9
b) (I) = I' (1;-1), phương trình đường tròn ảnh :
c) (I) = I'(3;2), phương trình đường tròn ảnh:
d) (I) = I'( -3;2), phương trình đường tròn ảnh:

Áp dụng Viet với lưu ý \(tanA+tanB+tanC=tanA.tanB.tanC\) ta có:
\(x_4+tanA+tanB+tanC=p\) (1)
\(x_4\left(tanA+tanB+tanC\right)+tanA.tanB+tanB.tanC+tanC.tanA=q\) (2)
\(x_4\left(tanA.tanB+tanB.tanC+tanC.tanA\right)+tanA.tanB.tanC=r\)(3)
\(x_4.tanA.tanB.tanC=s\) (4)
\(\left(1\right)\Rightarrow tanA+tanB+tanC=tanA.tanB.tanC=p-x_4\)
\(\left(4\right)\Rightarrow x_4\left(p-x_4\right)=s\)
Thế vào (2):
\(x_4\left(p-x_4\right)+tanA.tanB+tanB.tanC+tanC.tanA=q\)
\(\Rightarrow tanA.tanB+tanB.tanC+tanC.tanA=q-x_4\left(p-x_4\right)=q-s\)
Thế vào (3):
\(x_4\left(q-s\right)+p-x_4=r\)
\(\Rightarrow p-r=x_4\left(1-q+s\right)\Rightarrow x_4=\frac{p-r}{1-q+s}\)

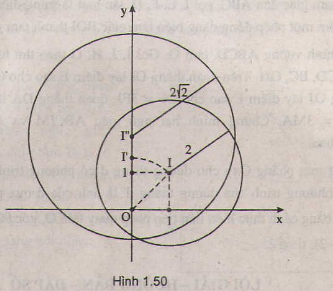
Phép quay tâm O, góc , biến I thành I'(0;
), phép vị tự tâm O, tỉ số
biến I' thành I'' = (0;
.
) = (0;2). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc
và phép vị tự tâm O, tỉ số
biến đường tròn (I;2) thành đường tròn (I'';2
). Phương trình của đường tròn đó là
+
= 8
Phép quay tâm O, góc , biến I thành I'(0;
), phép vị tự tâm O, tỉ số
biến I' thành I'' = (0;
.
) = (0;2). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc
và phép vị tự tâm O, tỉ số
biến đường tròn (I;2) thành đường tròn (I'';2
). Phương trình của đường tròn đó là
+
= 8