K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
22 tháng 10 2019
Tâm đối xứng của hình bình hành ABCD là giao điểm O của các đường chéo AC và BD.

CM
6 tháng 9 2018
AE//CG, AE = CG nên AECG là hình bình hành ⇒ O là trung điểm của EG. Tương tự O là trung điểm của HF.

8 tháng 8 2016
Bài 1:
Xét ΔADE và ΔCBF có:
AD=BC(gt)
\(\widehat{ADE}=\widehat{CBF}\) (soletrong do AD//BC)
DE=BF(gt)
=>ΔADE=ΔCBF(c.g.c)
=>AE=CF (1)
Xét ΔABF và ΔCDE có:
BF=DE(gt)
\(\widehat{ABF}=\widehat{CDE}\) (soletrong do AB..CD)
AB=CD(gt)
=>ΔABF=ΔCDE(c.g.c)
=>AF=CE (2)
Từ (1)(2) suy ra: AFCE là hbh
=>AF//CE
8 tháng 8 2016
XIN LỖI NẾU LM PHIỀN CÁC BN MK ĐANG CẦN GẤP GIẢI GIÙM NHÉ ![]()
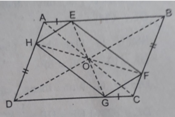
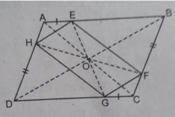
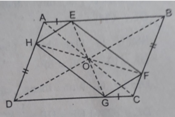
O còn là tâm đối xứng của các hình bình hành: AECG, EBGD, AHCF, DHBF.