
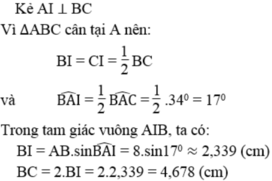
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


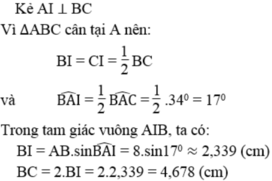

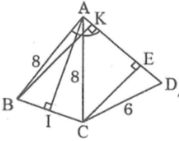
a) Kẻ AM vuong goc voi BC tai M
Tam giac BAC can tai A, co AM la duong cao=> AM cung la trung tuyen va phan giac cua tam giac ABC => MB=MC va goc BAM = goc CAM = 34/2=17 do
Xet tam giac AMB vuong tai M, ta co:
sin BAM = BM/AB => BM = AB.sinBAM = 8.sin(17 do)
Suy ra BC= 2.BM = 16.sin(17 do)
b) Ve CH vuong goc voi AD tai H
Xet tam giac AHC vuong tai H co:
sinCAD = CH/AC => CH= AC.sinCAD=8.sin(42 do)
Xet tam giac CHD vuong tai H co:
sin ADC = CH/CD = 8.sin(42 do)/6 => goc ADC = ( bam may tinh)
c) Ve BK vuong goc voi AD tai K( K nam giua A,D), nhu vay khoang cach tu B den AD chinh la BK
goc BAD= goc BAC + goc CAD = 34 +42 = 76 do
Xet tam giac AKB vuong tai K, ta co:
sinBAD = BK./AB => BK =AB. sinBAD = 8.sin(72 do)
a)Kẻ đường cao AH
Ta có AB = AC => tam giác ABC cân tại A
Nên đường cao AH vừa là phân giác, vừa là trung trực
Suy ra BAHˆBAH^ = CAHˆCAH^ = BACˆ2BAC^2 = 34023402 = 170170
Xét tam giác AHC vuông tại H, ta có:
sin CAHˆCAH^ = HCACHCAC => HC = sin CAHˆCAH^.AC = sin 170170.8 = 2,34
Do AH là trung trực của tam giác ABC nên BC = 2HC = 2.2,34 = 4,68
Vậy BC = 4,68cm
b) Kẻ CE vuông góc với AD
Xét tam giác ACE vuông tại E, ta có:
ADEˆADE^ = CEACCEAC => CE = sin CAEˆCAE^.AC = sin 420ˆ420^.8 = 5,353
Xét tam giác CED vuông tại E, ta có
sin CDEˆCDE^ = CECDCECD = 5,35365,3536 ≈≈ 0,8922
Suy ra CDEˆCDE^ = 63,15063,150 = 6306309'
Hay ADCˆADC^ = 63,15063,150
c) Ta có BADˆBAD^ = BACˆBAC^ + CADˆCAD^ = 340340 + 420420 = 760760
Kẻ BF vuông góc với AD
Xét tam giác BFA vuông tại F, ta có
BF = sin BADˆBAD^.AB = sin 760760.8 = 7,76
Vậy khoảng cách từ điểm B đến cạnh AD bằng 7,76cm

:v Làm bài 31 thôi nhá , còn lại all tự làm -..-
Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).
Diện tích tam giác ban đầu là \(\frac{1}{2}xy\left(cm^2\right)\)
+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)
Diện tích tam giác mới là : \(\frac{1}{2}\left(x+3\right)\left(y+3\right)\left(cm^2\right)\)
Diện tích tăng thêm 36 cm2 nên ta có p/trình :
\(\frac{1}{2}\left(x+3\right)\left(y+3\right)=\frac{1}{2}xy+36\)
\(\Leftrightarrow\left(x+3\right)\left(y+3\right)=xy+72\)
\(\Leftrightarrow xy+3x+3y+9=xy+72\)
\(\Leftrightarrow3x+3y=63\)
\(\Leftrightarrow x+y=21\)
+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).
Diện tích tam giác mới là : \(\frac{1}{2}\left(x-2\right)\left(y-4\right)\left(cm^2\right)\)
Diện tích giảm đi 26cm2 nên ta có phương trình :
\(\frac{1}{2}\left(x-2\right)\left(y-4\right)=\frac{1}{2}xy-26\)
\(\Leftrightarrow\left(x-2\right)\left(y-4\right)=xy-52\)
\(\Leftrightarrow xy-4x-2y+8=xy-52\)
\(\Leftrightarrow4x+2y=60\)
\(\Leftrightarrow2x+y=30\)
Ta có hệ phương trình : \(\hept{\begin{cases}x+y=21\\2x+y=30\end{cases}}\)
Lấy phương trình thứ hai trừ phương trình thứ nhất ta được :
\(\hept{\begin{cases}\left(2x+y\right)-\left(x+y\right)=30-21\\x+y=21\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+y-\left(x+y\right)=9\\x+y=21\end{cases}\Leftrightarrow\hept{\begin{cases}x=9\\y=12\end{cases}}}\)
Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm

Bài 1:
a: ĐKXĐ: x>0; x<>1
b: \(A=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}\right)\cdot\left(1+\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}=\dfrac{2}{\sqrt{x}-1}\)
c: Thay \(x=6+2\sqrt{5}\) vào A, ta được:
\(A=\dfrac{2}{\sqrt{5}+1-1}=\dfrac{2\sqrt{5}}{5}\)
d: Để |A|>A thì A>0
=>\(\sqrt{x}-1>0\)
hay x>1

Nhầm:
\(\left\{\begin{matrix}2x+3y=m\\-5x+y=-1\end{matrix}\right.\)
(1) trừ (2) nhân (3)
\(x=\frac{m+3}{17}>0\Rightarrow m>-3\) (*)
thế vào (2)
\(y=5.\frac{m+3}{17}-1=\frac{5m+15-17}{17}=\frac{5m-2}{17}>0\Rightarrow m>\frac{2}{5}\) (**)
Từ (*) và (**) có m>2/5
gọi x, y (km/h) lần lượt là vận tốc của xe ô tô xuất phát từ A và B (x, y >0)
khi đó: + quãng đường xe ô tô xuất phát từ A đi được là 3x
+quãng đường xe ô tô xuất phát từ B đi được là 3y
nên ta có : 3x+3y=210 \(\Leftrightarrow\)x+y = 70 (1)
vì vận tốc của xe xuất phát từ A lớn hơn xe xuất phát B 10km/h nên ta có phương trình: x-y =10 (2)
từ (1) và (2) => ta có hệ phương trình :\(\left\{\begin{matrix}x+y=70\\x-y=10\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{\begin{matrix}2x=80\\x-y=10\end{matrix}\right.\Leftrightarrow\)\(\left\{\begin{matrix}x=40\\40-y=10\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{\begin{matrix}x=40\left(thỏa\right)\\y=30\left(thỏa\right)\end{matrix}\right.\)
vậy vận tốc của 2 xe ô tô lần lượt là 40 km/h và 30 km/h