Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tham khảo:
c. Giao điểm thứ hai của đồ thị có hoành độ bằng -3 và tung độ bằng 9. Ta có : B(-3 ; 9).
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}0,2x^2-x=0\\y=x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(0,2x-1\right)=0\\y=x\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;1\right);\left(5;5\right)\right\}\)
Bài giải:
Vẽ đồ thị: y = 
x2
|
x |
-6 |
-3 |
0 |
3 |
6 |
|
y = |
12 |
3 |
0 |
3 |
12 |
y = -x + 6
- Cho x = 0 => y = 6.
- Cho y = 0 => x = 6.
Vẽ đồ thị: xem hình bên dưới.
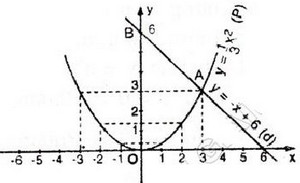
b) Giá trị gần đúng của tọa độ câc giao điểm (thực ra đây là giá trị đúng).
Hai đồ thị cắt nhau tại hai điểm A và B.
Theo đồ thị ta có A(3; 3) và B(-6; 12).
a) Vẽ đồ thị
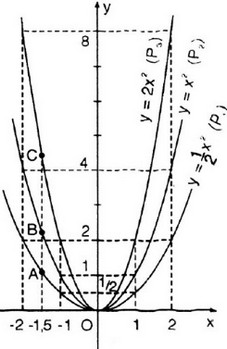
b) Gọi yA, yB, yC lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:
yA = 
. (-1,5)2 = . 2,25 = 1,125
yB = (-1,5)2 = 2,25
yC = 2 (-1,5)2 = 2 . 2,25 = 4,5
c) Gọi yA, yB, yC’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:
yA, = . 1,52 = . 2,25 = 1,125
yB, = 1,52 = 2,25
yC’ = 2 . 1,52 = 2 . 2,25 = 4,5
Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.
Vậy x = 0 thì hàm số có giả trị nhỏ nhất.
a: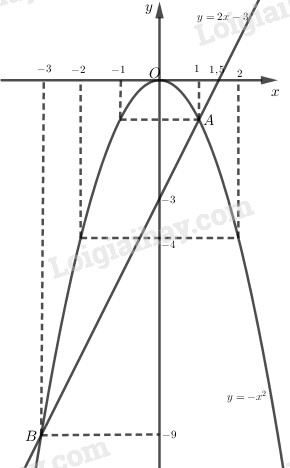 
b: Phương trình hoành độ giao điểm là:
\(2x-3+x^2=0\)
=>(x+3)(x-1)=0
=>x=-3 hoặc x=1
Khi x=-3 thì y=-9
Khi x=1 thì y=-1
c: Khi x=1 và y=-1 thì \(2\cdot1-3=-1=y\)
Khi x=-3 và y=-9 thì \(2\cdot\left(-3\right)-3=-9=y\)
Khi x=1 và y=-1 thì \(-x^2=-1=y\left(nhận\right)\)
Khi x=-3 và y=-9 thì \(-x^2=-9=y\left(nhận\right)\)
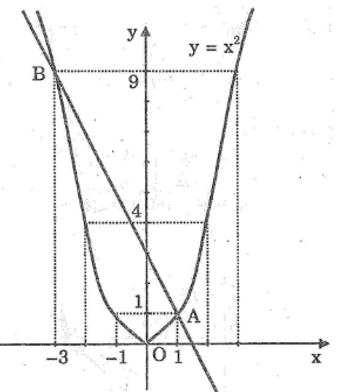
*Vẽ đồ thị hàm số y = x 2
Các giá trị của x và y :
y = -2x + 3
*Vẽ đồ thị hàm số y = -2x + 3
Cho x = 0 thì y = 3 ⇒ (0 ; 3)
Cho y = 0 thì x = 1,5 ⇒ (1,5 ; 0)