Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

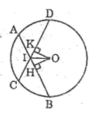
Xét hai tam giác OIH và OIK, ta có :
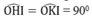
OI chung
OH = OK (chứng minh trên)
Suy ra: ∆ OIH = ∆ OIK (cạnh huyền, cạnh góc vuông)
Suy ra: IH = IK (1)
Lại có: HA = HB = (1/2).AB
KC = KD = (1/2).CD
Mà AB = CD nên HA = KC (2)
Từ (1) và (2) suy ra: IA = IC
Mà AB = CD nên IB = ID

Ta có: HA = HB (gt)
Suy ra : OH ⊥ AB (đường kính dây cung)
Lại có : KC = KD (gt)
Suy ra : OK ⊥ CD (đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH (dây lớn hơn gần tâm hơn)
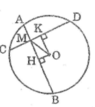
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
O M 2 = O H 2 + H M 2
Suy ra : H M 2 = O M 2 - O H 2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
O M 2 = O K 2 + K M 2
Suy ra: K M 2 = O M 2 - O K 2 (2)
Mà OH < OK (cmt) (3)
Từ (1), (2) và (3) suy ra: H M 2 > K M 2 hay HM > KM

có sđ AB = sđ BC = sđ CD
mà BIC = 1/2 ( sđ AD - sđ BC ) =1/2 ( sđ BD - sđ AB -sđ BC )
BKD = 1/2 ( sđ BD - sđ BC-sđ CD )
nên BIC=BKD
b,KBC = CDB ( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung CD)
mà CDB = CBD ( BC = CD )
nên KBC = CBD => BC là tia pg của KBD
A)
Vì góc BIC có đỉnh nằm ngoài đường tròn
nên: góc BIC = \(\dfrac{sđAD-sđBC}{2}\)
Mà: sđAD = \(\dfrac{sđBD+sđAB}{2}\) ; sđBC = sđ AB = sđCD
=> góc BIC = \(\dfrac{sđBD+sđAB-sđAB}{2}\) = \(\dfrac{sđBD}{2}\) (1)
Ta có: góc BKD = \(\dfrac{sđBD}{2}\) (2)
từ (1) và (2) => góc BIC = góc BKD
B)
Vì góc KBC và góc BDC cùng chắn cung BC
=> góc KBC = góc BDC (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung )
Ta có: sđBC = sđCD (gt)
nên: góc BDC = góc DBC (hai góc nội tiếp chắn hai cung bằng nhau)
Vậy góc KBC = góc DBC (cùng bằng góc BDC)
hay: BC là tia phân giác của góc DBK



Kẻ OH ⊥ AB, OK ⊥ CD
Ta có: AB = CD (gt)
Suy ra : OH = OK (hai dây bằng nhau cách đều tâm)
Vậy OI là tia phân giác của góc BID (tính chất đường phân giác)