Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Theo đề, ta có: \(x_1\cdot y_1=x_2\cdot y_2\)
\(\Leftrightarrow\dfrac{y_1}{5}=\dfrac{y_2}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{y_1}{5}=\dfrac{y_2}{2}=\dfrac{3y_1+4y_2}{3\cdot5+4\cdot2}=\dfrac{46}{23}=2\)
Do đó: \(y_1=10\)
\(k=xy=10\cdot2=20\)
=>y=20/x

Thời gian để đi 3 km bằng xe đạp là : 3 : 15 = 0,2 (giờ) Đổi : 0,2 giờ = 12 phút. Nếu bớt 3 km quãng đường từ nhà đến bưu điện thì thời gian đi cả hai quãng đường từ nhà đến trường và từ nhà đến bưu điện (đã bớt 3 km) là : 1 giờ 32 phút - 12 phút = 1 giờ 20 phút = 80 phút. Vận tốc đi xe đạp gấp vận tốc đi bộ là : 15 : 5 = 3 (lần) Khi quãng đường không đổi, vận tốc tỉ lệ nghịch với thời gian nên thời gian đi từ nhà đến trường gấp 3 lần thời gian đi từ nhà đến thư viện (khi đã bớt đi 3 km). Vậy : Thời gian đi từ nhà đến trường là : 80 : (1 + 3) x 3 = 60 (phút) ; 60 phút = 1 giờ Quãng đường từ nhà đến trường là : 1 x 5 = 5 (km)
quang dduong tu nha ban den truong la: 5km[ k cai nha tui k lai cho ha ]

Từ \(b^2=ac\Rightarrow\frac{a}{b}=\frac{b}{c}\)
\(c^2=bd\Rightarrow\frac{b}{c}=\frac{c}{d}\)
\(\Rightarrow\frac{a}{b}=\frac{b}{c}=\frac{c}{d}\)
\(\Rightarrow\left(\frac{a}{b}\right)^3=\left(\frac{b}{c}\right)^3=\left(\frac{c}{d}\right)^3\)
\(\Rightarrow\frac{a^3}{b^3}=\frac{b^3}{c^3}=\frac{c^3}{d^3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{a^3}{b^3}=\frac{b^3}{c^3}=\frac{c^3}{d^3}=\frac{a^3+b^3+c^3}{b^3+c^3+d^3}\left(1\right)\)
Lại có : \(\frac{a^3}{b^3}=\frac{a}{b}.\frac{a}{b}.\frac{a}{b}=\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=\frac{abc}{bcd}=\frac{a}{d}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\frac{a^3+b^3+c^3}{b^3+c^3+d^3}=\frac{a}{d}\left(đpcm\right)\)
Chúc bạn học tốt !!!
\(\frac{a+5}{a-5}=\frac{b+6}{b-6}\)
\(\Leftrightarrow\left(a+5\right)\left(b-6\right)=\left(b+6\right)\left(a-5\right)\)
\(\Leftrightarrow ab-6a+5b-30=ab-5b+6a-30\)
\(\Leftrightarrow ab-6a+5b-30-ab+5b-6a+30=0\)
\(\Leftrightarrow\left(ab-ab\right)-\left(6a+6a\right)+\left(5b+5b\right)-\left(30-30\right)=0\)
\(\Leftrightarrow10b-12a=0\)
\(\Leftrightarrow10b=12a\)
\(\Leftrightarrow\frac{a}{10}=\frac{b}{12}\)
\(\Leftrightarrow\frac{a}{5}=\frac{b}{6}\)
\(\Leftrightarrow\frac{a}{b}=\frac{5}{6}\left(đpcm\right)\)
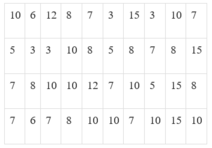
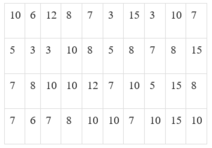
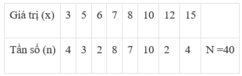
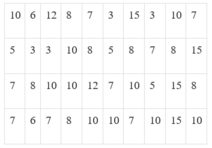

Chọn D