Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì cano đi từ A đến B mất 2giờ nên trong 1 giờ cano đi được \(\frac{1}{2}\)AB.
Cano đi từ B đến A mất 3 giờ nên trong 1 giờ cano đi được \(\frac{1}{3}\)AB.
Vận tốc cano từ A đến B hơn vận tốc cano từ B đến A là: \(\frac{1}{2}-\frac{1}{3}=\frac{1}{6}\) (quãng AB).
Vì hiệu vận tốc cano xuôi dòng và vận tốc cano ngược dòng bằng 2 lần vận tốc dòng nước nên 1 giờ khóm bèo trôi được là: \(\frac{1}{6}:2=\frac{1}{12}\) (quãng AB). Vậy thời gian để khóm bèo trôi từ A đến B là 12 giờ.
Vì cano đi từ A đến B mất 2 giờ nên trong 1 giờ cano đi được 1/2 AB.
Cano đi từ B đến A mất 3 giờ nên trong 1 giờ cano đi được 1/3 AB.
Vận tốc cano từ A đến B hơn vận tốc cano từ B đến A là: 1/2 - 1/3 = 1/6 (quãng AB).
Vì hiệu vận tốc cano xuôi dòng và vận tốc cano ngược dòng bằng 2 lần vận tốc dòng nước nên 1 giờ khóm bèo trôi được là:
1/6 : 2 = 1/12 (quãng AB).
Vậy thời gian để khóm bèo trôi từ A đến B là 12 giờ.

Bài 1:
Theo đề, ta có: \(x_1\cdot y_1=x_2\cdot y_2\)
\(\Leftrightarrow\dfrac{y_1}{5}=\dfrac{y_2}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{y_1}{5}=\dfrac{y_2}{2}=\dfrac{3y_1+4y_2}{3\cdot5+4\cdot2}=\dfrac{46}{23}=2\)
Do đó: \(y_1=10\)
\(k=xy=10\cdot2=20\)
=>y=20/x

Bài 1: a) 2333 và 3222
Ta có: 2333 = (23)111 = 8111
3222 = (32)111 = 9111
Ta thấy: 8111 < 9111 hay 2333 < 3222
b) 32009 và 91005
Ta có: 91005 = (32)1005 = 32.1005 = 32010
Ta thấy: 32009 < 32010 hay 32009 < 91005
c) 9920 và 999910
Ta có: 9920 = (992)10 = 980110
Ta thấy: 980110 < 999910 hay 9920 < 999910

Gọi vận tốc của ô tô nửa đoạn đường đầu là x, nửa đoạn đường cuối là y (y > x > 0)
Theo đề bài ta có: y = 20%x + x = \(\frac{1}{5}\)x + x = \(\frac{6}{5}\)x
\(\Rightarrow\frac{x}{y}=\frac{5}{6}\left(1\right)\)
Gọi thời gian đi nửa đoạn đường đầu ô tô đi là t1, thời gian nửa đoạn đường sau là t2 (t1 > t2 > 0)
=> t1 - t2 = \(\frac{10}{60}=\frac{1}{6}\left(h\right)\)
Ta có: x.t1 = y.t2 (cùng bằng \(\frac{1}{2}\) quãng đường AB)
\(\Rightarrow\frac{x}{y}=\frac{t_2}{t_1}\) kết hơp với (1) \(\Rightarrow\frac{t_2}{t_1}=\frac{5}{6}\Leftrightarrow\frac{t_2}{5}=\frac{t_1}{6}\)
Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{t_2}{5}=\frac{t_1}{6}=\frac{t_1-t_2}{6-5}=\frac{\frac{1}{6}}{1}=\frac{1}{6}\)
\(\Rightarrow\begin{cases}t_2=\frac{1}{6}.5=\frac{5}{6}\\t_1=\frac{1}{6}.6=1\end{cases}\)
Vậy thời gian thực tế ô tô đi hết quãng đường AB là:
t1 + t2 = 1 + \(\frac{5}{6}=\frac{11}{6}\) = 1h50'
Câu hỏi này không hỏi rõ là thời gian dự định hay thời gian thực tế mà đã làm rồi.

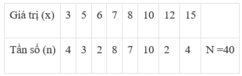
Chọn A