Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
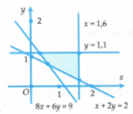
Gọi a, b lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua đảm bảo lượng protein và lipit trong thức ăn. Theo bài ra ta có số tiền gia đình cần trả là 160a + 110b với a, b thỏa mãn



Do đó, tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn thì x = a = 0,3; y = b = 1,1
![]()

ta có \(y'=\frac{m^2-9}{\left(x+m\right)^2}\) để hàm số đồng biến trên \(\left(2;+\infty\right)\) với m khác 3 thì y'>0 với mọi \(x\in\left(2;+\infty\right)\)
\(\Rightarrow m^2-9>0\) \(\Rightarrow m\in\left(-\infty;3\right)\cup\left(3;+\infty\right)\)
vậy ta đc đk của m

\(y'=3x^2-6x+m\)
để hàm số đồng biến trên R thì y'>0 với mọi x thuộc R
suy ra \(\begin{cases}3>0\\\Delta=9-3m<0\end{cases}\) suy ra m>3
vậy m>3 là điều cần tìm

Gọi số tự nhiên có 4 chữ số khác nhau đôi một được chọn từ các chữ số 0; 1; 2; 3;4;5;6 là a b c d .
a có 6 cách chọn; các số còn lại có A 6 3 cách chọn. Suy ra số phần tử của S là 6 . A 6 3 = 720
Do đó n Ω = 720
Gọi A là biến cố: “số được chọn là số chẵn đồng thời chữ số hàng đơn vị bằng tổng các chữ số hàng chục, trăm và nghìn”.
Số được chọn thỏa mãn yêu cầu đề bài nếu
d ∈ 0 ; 2 ; 4 ; 6 d = a + b + c ⇒ d ∈ 4 ; 6 d = a + b + c .
* Trường hợp 1: Số có dạng a b c 4 với a + b + c = 4 suy ra tập { a;b;c } là { 0;1;3 }. Vì a,b,c đôi một khác nhau nên có 2 cách chọn a; 2 cách chọn b; 1 cách chọn c. Do đó số các số thuộc dạng này là 2 . 2 . 1 = 4
* Trường hợp 2: Số có dạng a b c 6 với a + b + c = 6 suy ra tập { a;b;c } có thể là một trong các tập { 0;1;5 }; { 0;2;4 }; { 1;2;3 }
+ Nếu { a;b;c } là tập { 0;1;5 } hoặc { 0;2;4 } thì mỗi trường hợp có 4 số (tương tự trường hợp trên)
+ Nếu { a;b;c } là tập { 1;2;3 } thì có P 3 = 3! = 6 số.
Do đó số các số thuộc dạng này là 4 + 4 + 6 = 14
Qua hai trường hợp trên, ta suy ra n(A): = 14 + 4 = 18.
Vậy xác suất cần tìm là
P A = n A n Ω = 18 720 = 1 40
Đáp án C


Đáp án A
Cuối tháng 1, mẹ nhận được số tiền là 4 . 10 6 . 1 + 1 % đồng.
Cuối tháng 2, mẹ nhận được số tiền là
4 . 10 6 . 1 + 1 % + 4 . 10 6 . 1 + 1 % = 4 . 10 6 . 1 + 1 % 2 + 1 + 1 %
Cuối tháng 3, mẹ nhận được số tiền là 4 . 10 6 . 1 + 1 % 3 + 1 + 1 % 2 + 1 + 1 % đồng.
... ... ...
Vậy hàng tháng mẹ gửi vào ngân hàng a đồng, lãi suất r% và số tiền thu được sau n tháng là A = a r . 1 + r . 1 + r n - 1 . Suy ra sau 11 tháng, mẹ lĩnh được A = 4 . 10 6 1 % . 1 + 1 % . 1 + 1 % 11 - 1 .
Vì đầu tháng 12 mẹ mới rút tiền nên mẹ được cộng thêm cả tiền lương của tháng 12.
Vậy tổng số tiền mẹ nhận được là A + 4 . 10 6 = 50 triệu 730 nghìn đồng.

Tổng số tiền Nam nợ ngân hàng sau 4 năm là
10 1 + 0 , 04 4 + 10 1 + 0 , 04 3 + 10 1 + 0 , 04 2 + 10 1 + 0 , 04 1 ≈ 44 , 163 triệu đồng.
Chọn đáp án B.

Đáp án C.
Phương pháp:
Công thức lãi kép, không kỳ hạn: A n = M 1 + r % n
Với: A n là số tiền nhận được sau tháng thứ n,
M là số tiền gửi ban đầu,
n là thời gian gửi tiền (tháng),
r là lãi suất định kì (%)
Cách giải:
Thời gian người đó gửi: 15/4/2018 đến 15/3/2020 tương ứng với 23 tháng.
Ta có: A n = M 1 + r % n ⇔ 50 000 000 = M 1 + 0 , 55 % 23 ⇒ M ≈ 44 704 000 (đồng)

Đáp án C.
Điều kiện x > 2 ; x ≠ 4. Phương trình tương đương log 3 x − 2 2 + log 3 x − 4 2 = 0
⇔ log 3 x − 2 2 x − 4 2 = 0 ⇔ x − 2 2 x − 4 2 = 1 ⇔ x = 3.