
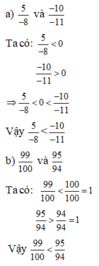
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

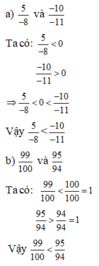

Bài 1 :
\(A=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{50-49}{49.50}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{3}+...+\frac{1}{49}-\frac{1}{50}\)
\(=1-\frac{1}{50}< 1\left(1\right)\)
\(B=\frac{1}{10}+\left(\frac{1}{11}+\frac{1}{12}+...+\frac{1}{99}+\frac{1}{100}\right)\)\(>\frac{1}{10}+\frac{1}{100}.90=1\left(2\right)\)
Từ (1) và ( 2) ta có \(A< 1\) \(B>1\)NÊN \(A< B\)
Bài 2:
\(S=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\)
\(=\frac{\left(a+b+c\right)-\left(b+c\right)}{b+c}+\)\(\frac{\left(a+b+c\right)-\left(c+a\right)}{c+a}\)\(+\frac{\left(a+b+c\right)-\left(a+b\right)}{a+b}\)
\(=\frac{7-\left(b+c\right)}{b+c}+\frac{7-\left(c+a\right)}{c+a}+\frac{7-\left(a+b\right)}{a+b}\)
\(=7.\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right)-3\)
\(=7.\frac{7}{10}-3\)\(=\frac{49}{10}-3=\frac{19}{10}\)
\(S=\frac{19}{10}>\frac{19}{11}=1\frac{8}{11}\)
Chúc bạn học tốt ( -_- )
Bài 1:
ta có: \(A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{49.50}\)
\(A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{49}-\frac{1}{50}\)
\(A=1-\frac{1}{50}< 1\)
\(\Rightarrow A< 1\)(1)
ta có: \(\frac{1}{11}>\frac{1}{100};\frac{1}{12}>\frac{1}{100};...;\frac{1}{99}>\frac{1}{100}\)
\(\Rightarrow\frac{1}{11}+\frac{1}{12}+...+\frac{1}{99}+\frac{1}{100}>\frac{1}{100}+\frac{1}{100}+...+\frac{1}{100}+\frac{1}{100}\) ( có 90 số 1/100)
\(=\frac{90}{100}=\frac{9}{10}\)
\(\Rightarrow B=\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+...+\frac{1}{99}+\frac{1}{100}>\frac{1}{10}+\frac{9}{10}=1\)
\(\Rightarrow B>1\)(2)
Từ (1);(2) => A<B

a) \(\frac{8}{9}=1-\frac{1}{9}\)
\(\frac{108}{109}=1-\frac{1}{109}\)
Vì \(\frac{1}{9}>\frac{1}{109}\)
Nên \(1-\frac{1}{9}< 1-\frac{1}{109}\)
Vậy \(\frac{8}{9}< \frac{108}{109}\)
b)
\(\frac{97}{100}=\frac{97\cdot99}{100\cdot99}\)
\(\frac{98}{99}=\frac{98\cdot100}{99\cdot100}\)
\(\Rightarrow\frac{97}{100}< \frac{98}{99}\)

Lời giải:
a. $\frac{-10}{-11}=\frac{10}{11}>0 >\frac{5}{-8}$
b.
$\frac{99}{100}< 1< \frac{95}{94}$

1. a) Để \(A=\frac{3n+5}{n+1}\)là phân số thì \(n+1\ne0\Leftrightarrow n\ne-1\)
Vậy ...
b) Để A là ps thì \(3n+5⋮n+1\)
Ta có: \(3n+5=3\left(n+1\right)+2\)
Vì \(3\left(n+1\right)⋮n+1\)nên để \(3n+5⋮n+1\)thì \(2⋮n+1\Leftrightarrow n+1\varepsilonƯ\left(2\right)\)
Bạn tự tìm n nha rồi kết luận


Giải như mà mình không chắc nha:
a) \(A=\frac{10^8+1}{10^9+1}\)và \(\frac{10^9+1}{10^{10}+1}\)
Ta có:
\(\frac{10^8+1}{10^9+1}\Leftrightarrow\frac{10^8+1}{10^8+10+1}\Leftrightarrow\frac{1}{10+1}=\frac{1}{11}\)
\(\frac{10^9+1}{10^{10}+1}=\frac{10^8+10+1}{10^8+10+10+1}=\frac{10+1}{10+10+1}=\frac{11}{21}\)
Ta có: \(\frac{1}{11}< \frac{11}{21}\) Vậy ......
b) Bạn giải tương tự nha! Lười lắm :v

+1 với +5 bên A bằng với bên B nên ta chỉ so sánh 126^99/12^100 bên A và 12^100/12^101 bên B
Vì 12^99[A]<12^100[B] và 12^100[A]<12^101[B]
=>A<B