Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B

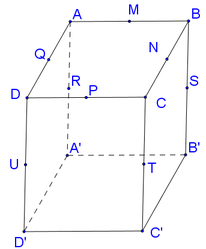
Gọi M, N, P, Q lần lượt là trung điểm của BB’, AA’, DD’, CC’
Khi đó mặt phẳng (P) thỏa yêu cầu bài toán chính là mặt phẳng (MNPQ)
Qua phép đối xứng của mặt phẳng (P) thì tứ giác ADC'B' biến thành A'D'CB

a) Xét đường thẳng d qua M và d ⊥ (α).
Khi đó H chính là giao điểm của d và (α).
Vectơ (1 ; 1 ; 1) là vectơ pháp tuyến của (α) nên
là vectơ chỉ phương của d.
Phương trình tham số của đường thẳng d có dạng: .
Thay tọa độ x ; y ; z của phương trình trên vào phương trình xác định (α), ta có:
3t + 6 = 0 => t = -2 => H(-1 ; 2 ; 0).
b) Gọi M'(x ; y ; z) là điểm đối xứng của M qua mặt phẳng (α), thì hình chiếu vuông góc H của M xuống (α) chính là trung điểm của MM'.
Ta có:
=> x = -3 ;
=> y = 0 ;
=> z = -2.
Vậy M'(-3 ; 0 ;2).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α) bằng 2 cách sau:
Cách 1: Áp dụng công thức ta có:
.
Cách 2: Khoảng cách từ M đến (α) chính là khoảng cách MH:
d(M,(α) )= MH = .

a) Xét đường thẳng d qua M và d ⊥ (α).
Khi đó H chính là giao điểm của d và (α).
Vectơ (1 ; 1 ; 1) là vectơ pháp tuyến của (α) nên
là vectơ chỉ phương của d.
Phương trình tham số của đường thẳng d có dạng: .
Thay tọa độ x ; y ; z của phương trình trên vào phương trình xác định (α), ta có:
3t + 6 = 0 => t = -2 => H(-1 ; 2 ; 0).
b) Gọi M'(x ; y ; z) là điểm đối xứng của M qua mặt phẳng (α), thì hình chiếu vuông góc H của M xuống (α) chính là trung điểm của MM'.
Ta có:
=> x = -3 ;
=> y = 0 ;
=> z = -2.
Vậy M'(-3 ; 0 ;2).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α) bằng 2 cách sau:
Cách 1: Áp dụng công thức ta có:
.
Cách 2: Khoảng cách từ M đến (α) chính là khoảng cách MH:
d(M,(α) )= MH = .

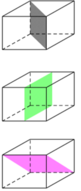
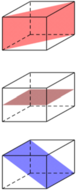
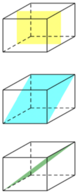
Hình lập phương có 9 mặt phẳng đối xứng: 3 mặt phẳng đối xứng chia nó thành hai khối hộp chữ nhật, 6 mặt phẳng đối xứng chia nó thành 2 khối lăng trụ tam giác.
Chọn B.
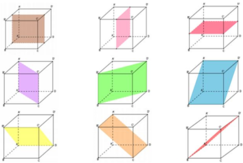

Đáp án D