Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lập các phân số rồi quy đồng mẫu các phân số vừa tìm được. Cũng có thể so sánh một số phân số đơn giản hơn với nhau rồi chọn phân số lớn nhất trong chúng để so sánh với những phân số còn lại.
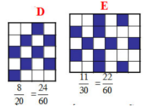
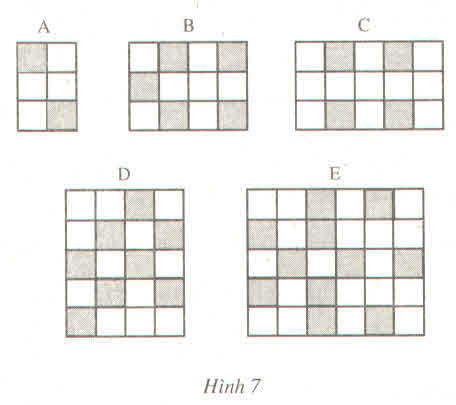
ĐS. a) b) Lưới E sẫm nhất.
a, Lập các phân số rồi quy đồng mẫu các phân số vừa tìm được. Cũng có thể so sánh một số phân số đơn giản hơn với nhau rồi chọn phân số lớn nhất trong chúng để so sánh với những phân số còn lại.
Ta được: .
b, Từ câu a ta kết luận: Lưới E sẫm nhất.

\(\frac{n+5}{n+1}=\frac{n+1+4}{n+1}=\frac{n+1}{n+1}+\frac{4}{n+1}=1+\frac{4}{n+1}\)
Để \(\frac{4}{n+1}\in N\) thì \(n+1\in\text{Ư}\left(4\right)=\left\{1;2;4\right\}\)
- \(n+1=1\Rightarrow n=0\)
- \(n+1=2\Rightarrow n=1\)
- \(n+1=4\Rightarrow n=3\)
Vậy \(n\in\left\{0;1;3\right\}\)

Gọi phân số tối giản cần tìm là \(\dfrac{a}{b}\)
Ta có:\(\dfrac{a}{b}\):\(\dfrac{5}{11}\)=\(\dfrac{11a}{5b}\)
\(\dfrac{a}{b}\):\(\dfrac{11}{21}\)\(\dfrac{21a}{11b}\)
\(\dfrac{a}{b}\):\(\dfrac{25}{28}\)=\(\dfrac{28a}{25b}\)
Vì cả 3 thương trên là số tự nhiên nên a chia hết cho 5,11,25\(\)\(\Rightarrow\)a\(\in\)BCNN(5;11;25)\(\Rightarrow\)a=275
Do đó b\(\in\)ƯCLN(11,21,28)=1
Vậy phân số tối giản cần tìm là \(\dfrac{275}{1}\)

theo phân số: 55/21;134/43;116/37;77/21
theo số thập phân:2.(619047); 3.(11627...); 3.(135); 4.(0526...)
Like nha !

ta có ab3=3/4.3ab
=> 3.ab3=4.3ab
=> 3.(100a+10b+3)=4.(300+10a+b)
= 300a+30b+9=1200+40a+4b
=>(300a-40a)+(30b-4b)=1200-9
=260a+26b=1196
=26.(10a+b)=1196
=>10a+b=1196:26
=10a+b=46
=>10a+b=10.4+6
=>a=4:b=6

Giải:
Đo độ dài các đoạn thẳng ta được: AB=30mm; BC= 35mm; AC= 18mm. Vậy AC<AB<BC.


 tang ban ne
tang ban ne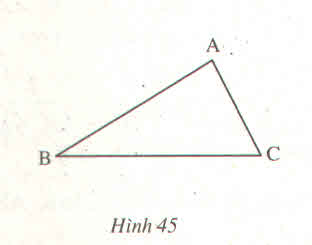
Sắp xếp:
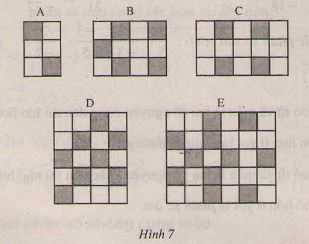
Vậy lưới sẫm nhất là lưới ở hình B.