
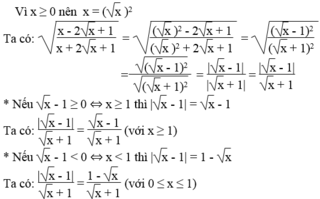
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

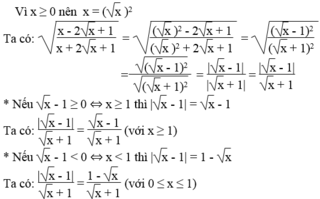

\(P=\frac{x+2}{\sqrt{x}^3-1}+\frac{\sqrt{x}+1}{x+\sqrt{x}+1}-\frac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(P=\frac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\frac{\sqrt{x}+1}{x+\sqrt{x}+1}-\frac{1}{\sqrt{x}-1}\)
\(P=\frac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
2,
\(A=\frac{5\left(\sqrt{7}-\sqrt{2}\right)}{\left(\sqrt{7}-\sqrt{2}\right)\left(\sqrt{7}+\sqrt{2}\right)}+\frac{\sqrt{2}+1}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}-\frac{7\sqrt{7}}{7}\)
\(A=\frac{5\left(\sqrt{7}-\sqrt{2}\right)}{7-2}+\frac{\left(\sqrt{2}+1\right)}{2-1}-\sqrt{7}\)
\(A=\sqrt{7}-\sqrt{2}+\sqrt{2}+1-\sqrt{7}=1\)
\(P=\frac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\frac{\sqrt{x}}{x+\sqrt{x}+1}\)

\(P=\frac{1}{x^2-\sqrt{x}}:\frac{\sqrt{x}+1}{x\sqrt{x}+x+\sqrt{x}}\)\(=\frac{1}{\sqrt{x}\left(\sqrt{x^3}-1^3\right)}:\frac{\sqrt{x}+1}{\sqrt{x}\left(x+\sqrt{x}+1\right)}\)
\(\frac{1}{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\frac{\sqrt{x}\left(x+\sqrt{x}+1\right)}{\sqrt{x}+1}\)\(\frac{1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\frac{1}{x-1}\)
2) De 3P=1+x
=> \(3\left(\frac{1}{x-1}\right)=x+1\)<=>\(\frac{3}{x-1}=x+1\)<=>\(\left(x+1\right)\left(x-1\right)=3\)
<=> \(x^2-1=3\)<=> \(x^2=4\)<=> \(x=2\)hoac \(x=-2\)
Vay voi x =2 va x=-2 ta co 3P=x+1

ĐK để phân thức XĐ : x khác 1 và x> 0
Đặt \(B=\left(\frac{\left(\sqrt{x}+2\right)\left(x-1\right)-\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+1\right)}{\left(x+2\sqrt{x}+1\right)\left(x-1\right)}\right)\) ( Đây là mình vừa đặt vừa làm mẫu thức chung nhe)
=> \(B=\left(\frac{x\sqrt{x}-\sqrt{x}+2x-2-x\sqrt{x}-2x-\sqrt{x}+2x+4\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2\left(x-1\right)}\right)\)
=>\(B=\frac{2\sqrt{x}+2x}{\left(\sqrt{x}+1\right)^2\left(x-1\right)}=\frac{2\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\left(x-1\right)}=\frac{2\sqrt{x}}{\left(\sqrt{x}+1\right)\left(x-1\right)}\)
A = \(B:\frac{\sqrt{x}}{\sqrt{x+1}}=\frac{2\sqrt{x}}{\left(\sqrt{x}+1\right)\left(x-1\right)}\cdot\frac{\sqrt{x}+1}{\sqrt{x}}=\frac{2}{x-1}\)
B, Bạn tự làm ý B nhe
HD để A nguyên => x - 1 thuộc ước của 2 mà 2 có các ước là +-1 và +-2
(+) với x-1 = 2 => x = 3
............................

\(a,A=\sqrt{27}+\frac{2}{\sqrt{3}-2}-\sqrt{\left(1-\sqrt{3}\right)^2}\)
\(=3\sqrt{3}+\frac{2\left(\sqrt{3}+2\right)}{\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)}-\left(\sqrt{3}-1\right)\)
\(=3\sqrt{3}+\frac{2\sqrt{3}+4}{3-4}-\sqrt{3}+1\)
\(=3\sqrt{3}-2\sqrt{3}-4-\sqrt{3}+1\)
\(=-3\)
\(B=\left(\frac{1}{x-\sqrt{x}}+\frac{1}{\sqrt{x}-1}\right):\frac{\sqrt{x}+1}{x-2\sqrt{x}+1}\)
\(=\left(\frac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\frac{1}{\sqrt{x}-1}\right):\frac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\)
\(=\frac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}.\frac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}\)
\(=\frac{\sqrt{x}-1}{\sqrt{x}}\)
b, Ta có \(B< A\)
\(\Leftrightarrow\frac{\sqrt{x}-1}{\sqrt{x}}< -3\)
\(\Leftrightarrow\frac{\sqrt{x}-1}{\sqrt{x}}+3< 0\)
\(\Leftrightarrow\frac{\sqrt{x}-1+3\sqrt{x}}{\sqrt{x}}< 0\)
\(\Leftrightarrow\frac{4\sqrt{x}-1}{\sqrt{x}}< 0\)
\(\Leftrightarrow4\sqrt{x}-1< 0\left(Do\sqrt{x}>0\right)\)
\(\Leftrightarrow\sqrt{x}< \frac{1}{4}\)
\(\Leftrightarrow0< x< \frac{1}{2}\)(Kết hợp ĐKXĐ)
Vậy ...

\(1,P=\frac{x+2}{x\sqrt{x}-1}+\frac{\sqrt{x}+1}{x+\sqrt{x}+1}-\frac{\sqrt{x}+1}{x-1}\)
\(=\frac{x+2}{x\sqrt{x}-1}+\frac{\sqrt{x}+1}{\left(x+\sqrt{x}+1\right)}-\frac{\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\frac{x+2}{x\sqrt{x}-1}+\frac{\sqrt{x}+1}{\left(x+\sqrt{x}+1\right)}-\frac{1}{\sqrt{x}-1}\)
\(=\frac{x+2}{x\sqrt{x}-1}+\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(x+\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\frac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\frac{x+2+x-1-x-\sqrt{x}-1}{x\sqrt{x}-1}\)
\(=\frac{x-\sqrt{x}}{x\sqrt{x}-1}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\frac{\sqrt{x}}{x+\sqrt{x}+1}\)

P\(=\left(\frac{x-\sqrt{x}+1-x}{x-\sqrt{x}+1}\right).\left(\frac{\sqrt{x^3}+1}{x+2\sqrt{x}+1}\right) \)
\(=\frac{1-\sqrt{x}}{x-\sqrt{x}+1}.\frac{\left(\sqrt{x}+1\right).\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2}\)
\(\frac{1-\sqrt{x}}{\sqrt{x}+1}\)