
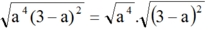
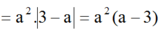
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

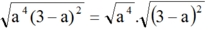
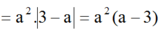
![]()

a, = \(\sqrt{a^2b^2.\left(1+\frac{1}{a^2b^2}\right)}\) = \(\sqrt{a^2b^2+1}\)
c, = \(\sqrt{\frac{a+ab}{b^4}}\) = \(\frac{\sqrt{a+ab}}{b^2}\)
k mk nha
a, \(ab\sqrt{1+\frac{1}{a^2b^2}}\)
\(ab\sqrt{1+\frac{1}{a^2b^2}}=ab\sqrt{\frac{1+a^2b^2}{a^2b^2}}=\frac{ab}{\left|ab\right|}\sqrt{1+a^2b^2}\)
\(=\hept{\begin{cases}\sqrt{1+a^2b^2}ĐK:ab>0\\-\sqrt{1+a^2b^2}ĐKab< 0\end{cases}}\)
b, \(\sqrt{\frac{a}{b^3}+\frac{a}{b^4}}\)
\(\sqrt{\frac{a}{b^3}+\frac{a}{b^4}}=\sqrt{\frac{a+ab}{b^4}}=\frac{1}{b^2}\sqrt{a+ab}\)

\(a,\frac{a-4\sqrt{a}+4-1}{\sqrt{a}-3}=\frac{\left(\sqrt{a}-2\right)^2-1}{\sqrt{a}-3}.\)
\(=\frac{\left(\sqrt{a}-3\right)\left(\sqrt{a}-1\right)}{\sqrt{a}-3}\)
\(=\sqrt{a}-1\)
\(b,\frac{a+\sqrt{a^2-6a+9}}{2a-3}=\frac{a+\sqrt{\left(a-3\right)^2}}{2a-3}\)
\(=\frac{a+a-3}{2a-3}=\frac{2a-3}{2a-3}\)
\(=1\)

a) \(\sqrt{2+\sqrt{3}}.\sqrt{2-\sqrt{3}}=\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}=\sqrt{4-3}=\sqrt{1}=1\)
b)
Đặt \(B=\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\)
\(B^2=4+\sqrt{7}-2\sqrt{\left(4+\sqrt{7}\right)\left(4-\sqrt{7}\right)}+4-\sqrt{7}\)
\(=8-2\sqrt{16-7}=8-2\sqrt{9}=8-2.3=8-6=2\)
\(\Rightarrow B=\sqrt{2}\)


A=\(\frac{u-v}{\sqrt{u}+\sqrt{v}}-\frac{\sqrt{u^3}+\sqrt{v^3}}{u-v}=\frac{\left(\sqrt{u}-\sqrt{v}\right)\left(\sqrt{u}+\sqrt{v}\right)}{\sqrt{u}+\sqrt{v}}-\frac{\left(\sqrt{u}+\sqrt{v}\right)\left(u-\sqrt{u}\sqrt{v}+v\right)}{\left(\sqrt{u}+\sqrt{v}\right)\left(\sqrt{u}-\sqrt{v}\right)}\)
\(=\sqrt{u}-\sqrt{v}-\frac{u-\sqrt{uv}+v}{\sqrt{u}-\sqrt{v}}=\frac{u-2\sqrt{uv}+v-u+\sqrt{uv}-v}{\sqrt{u}-\sqrt{v}}=\frac{-\sqrt{uv}}{\sqrt{u}-\sqrt{v}}\)


a)
\(\sqrt{\left(3-2\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{8}-4\right)^2}=3-2\sqrt{2}-4+\sqrt{8}\)
\(=3-2\sqrt{2}-4+2\sqrt{2}=3-4=-1\)
b)
\(\frac{2}{\sqrt{3}-1}-\frac{2}{\sqrt{3}+1}=\frac{2\left(\sqrt{3}+1\right)-2\left(\sqrt{3}-1\right)}{3-1}\)
\(=\frac{2\left(\sqrt{3}+1-\sqrt{3}+1\right)}{2}=\sqrt{3}+1-\sqrt{3}+1=1+1=2\)

a) ĐS: .
b) ĐS: Nếu thì
Nếu ab
c) ĐS:
d)
Nhận xét. Nhận thấy rằng để có nghĩa thì
Do đó
. Vì thế có thể phân tích tử thành nhân tử.
a) ĐS: .
b) ĐS: Nếu thì
Nếu ab
c) ĐS:
d)
Nhận xét. Nhận thấy rằng để có nghĩa thì
Do đó
. Vì thế có thể phân tích tử thành nhân tử.