
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

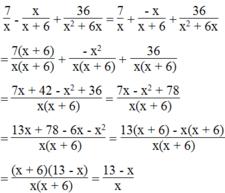

= ( x/(x-6)(x+6) - x-6/x(x+6) ) : 2x-6/x2 + 6x + 6/6-x
=( x2/x(x+6)(x-6) - (x -6 )(x-6)/x(x+6)(x-6) ) : .....
= (12x -36 / x(x+6)(x-6) : 2x-6/ x2 + 6x )+ 6/6-x
=6/x-6 + 6/6-x
= 6-6/ x-6
=0/x-6
câu trước mình thiếu 6/6-x

a)
DK:tồn tại P \(\hept{\begin{cases}x\ne0\\x\ne-+6\\x\ne3\end{cases}}\)
\(P=\left(\frac{x}{\left(x-6\right)\left(x+6\right)}-\frac{x-6}{x\left(x+6\right)}\right).\frac{x\left(x+6\right)}{2\left(x-3\right)}\\ \)
\(P=\left(\frac{x^2-\left(x-6\right)\left(x-6\right)}{x\left(x-6\right)\left(x+6\right)}\right).\frac{x\left(x+6\right)}{2\left(x-3\right)}\)
\(P=\left(\frac{x^2-\left(x^2-12x+36\right)}{x\left(x-6\right)\left(x+6\right)}\right).\frac{x\left(x+6\right)}{2\left(x-3\right)}\)
\(P=\left(\frac{12\left(x-3\right)}{x\left(x-6\right)\left(x+6\right)}\right).\frac{x\left(x+6\right)}{2\left(x-3\right)}=\frac{6}{x-6}\)
b)6/(x-6)=1=> x-6=6=> x=12
c)x-6<0=> x<6

a/ S=\(\left(\frac{x}{\left(x+6\right)\left(x-6\right)}-\frac{x-6}{x\left(x+6\right)}\right).\frac{x\left(x+6\right)}{2x-6}-\frac{x}{x-6}\)
S=\(\frac{x^2-\left(x-6\right)^2}{x\left(x+6\right)\left(x-6\right)}.\frac{x\left(x+6\right)}{2x-6}-\frac{x}{x-6}\)=\(\frac{\left(x-x+6\right)\left(x+x-6\right)}{\left(x-6\right)\left(2x-6\right)}-\frac{x}{x-6}\)
= \(\frac{6\left(2x-6\right)}{\left(x-6\right)\left(2x-6\right)}-\frac{x}{x-6}\)= \(\frac{6}{\left(x-6\right)}-\frac{x}{x-6}\)\(\frac{6-x}{x-6}=-1\)
b/ S luôn =-1 với mọi x

tôi cũng cung thiên yết nè nhưng lại là cậu bé mà thiên yết hợp với cung gì nhất vậy add friend nha

\(1,ĐK:x\ne0;x\ne\pm6\)
\(A=\left[\frac{6x+1}{x\left(x-6\right)}+\frac{6x-1}{x\left(x+6\right)}\right].\frac{\left(x+6\right)\left(x-6\right)}{12\left(x^2+1\right)}\)
\(=\frac{6x^2+36x+x+6+6x^2-36x-x+6}{x}.\frac{1}{12\left(x^2+1\right)}\)
\(=\frac{12\left(x^2+1\right)}{x}.\frac{1}{12\left(x^2+1\right)}=\frac{1}{x}\)
\(2,A=\frac{1}{x}=\frac{1}{\frac{1}{\sqrt{9+4\sqrt{5}}}}=\sqrt{9+4\sqrt{5}}\)
Cho tam giác ABC vuông tại B có góc B1=B2 ; Â=60o, kẻ BH vuông góc với AC (H thuộc AC). Qua B kẻ đường thẳng d song song với AC.
a) Tính góc ABH.
b) Chứng minh đường thẳng d vuông góc với BH.

Mình thử nha :33
ĐKXĐ : \(x\ne-3,x\ne-26,x\ne-6,x\ne1\)
Ta có :
\(A=\left[\frac{3}{2}-\left(\frac{x^4\left(x^2+1\right)-x^4-1}{x^2+1}\right)\cdot\frac{x^3-4x^2+\left(x-4\right)}{x^6\left(x+6\right)-\left(x+6\right)}\right]:\frac{\left(x+3\right)\left(x+26\right)}{3\left(x-2\right)\left(x+6\right)}\)
\(=\left[\frac{3}{2}-\left(\frac{x^6-1}{x^2+1}\right)\cdot\frac{\left(x-4\right)\left(x^2+1\right)}{\left(x+6\right)\left(x^6-1\right)}\right]\cdot\frac{3\left(x-2\right)\left(x+6\right)}{\left(x+3\right)\left(x+26\right)}\)
\(=\left[\frac{3}{2}-\frac{x-4}{x+6}\right]\cdot\frac{3\left(x-2\right)\left(x+6\right)}{\left(x+3\right)\left(x+26\right)}\)
\(=\frac{x+26}{2\left(x+6\right)}\cdot\frac{3\left(x-2\right)\left(x+6\right)}{\left(x+3\right)\left(x+26\right)}\)
\(=\frac{3\left(x-2\right)}{2\left(x+3\right)}\)
Vậy : \(A=\frac{3\left(x-2\right)}{2\left(x+3\right)}\left(x\ne-3,x\ne-26,x\ne-6,x\ne1\right)\)

\(A=\left(\dfrac{x}{\left(x-6\right)\left(x+6\right)}-\dfrac{x-6}{x\left(x+6\right)}\right)\cdot\dfrac{x\left(x+6\right)}{2x-6}-\dfrac{x}{x-6}\)
\(=\dfrac{x^2-x^2+12x-36}{x\left(x-6\right)\left(x+6\right)}\cdot\dfrac{x\left(x+6\right)}{2\left(x-3\right)}-\dfrac{x}{x-6}\)
\(=\dfrac{12\left(x-3\right)}{x-6}\cdot\dfrac{1}{2\left(x-3\right)}-\dfrac{x}{x-6}\)
\(=\dfrac{12}{2\left(x-6\right)}-\dfrac{x}{x-6}=\dfrac{6-x}{x-6}=-1\)

Đặt \(A=\frac{x^2+x-6}{x^3-4x^2-18x+9}\)
\(A=\frac{x^2+3x-2x-6}{x^3+3x^2-7x^2-21x+3x+9}\)
\(A=\frac{x\left(x+3\right)-2\left(x+3\right)}{x^2\left(x+3\right)-7x\left(x+3\right)+3\left(x+3\right)}\)
\(A=\frac{\left(x-2\right)\left(x+3\right)}{\left(x^2-7x+3\right)\left(x+3\right)}\)
\(A=\frac{x-2}{x^2-7x+3}\)