
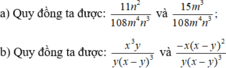
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

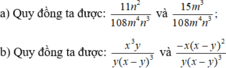

1/ a/ 5x2 - 20
= 5.(x2 - 4)
=5.(x2 - 22)
=5.(x+2).(x-2)
b/ xy2 - y3 - x + y
= (xy2 - x) - (y3 - y)
= x(y2 - 1) - y(y2 - 1)
= (y2 - 1).(x-y)
= (y-1).(y+1).(x-y)
c/ x2 + 3x - 10
= x2 + 5x - 2x - 10
= x(x+5) - 2(x+5)
= (x+5).(x-2)
d/ x2 - y2 + 12y - 36
= x2 - (y2 - 2.y.6 + 62)
= x2 - (y-6)2
= (x+y-6).(x-y+6).
2/ a/ 4x2 - 9 - x(2x-3) = 0
(2x)2 - 32 - x(2x-3) = 0
(2x+3).(2x-3)-x(2x-3) = 0
(2x-3).(2x+3-x) = 0
(2x-3).(x+3) = 0
=> 2x - 3 = 0 hoặc x + 3 = 0
hay x = 3/2 hoặc x = -3
b/ x3 -25x = 0
x(x2 - 25) = 0
x(x+5)(x-5) = 0
=> x = 0 hoặc x+5=0 hoặc x-5 = 0
hay x = 0; x = -5; x = 5
c/ 2(x+5) - x2 - 5x = 0
2(x+5) - x(x+5) = 0
(x+5).(2-x) = 0
=> x + 5 = 0 hoặc 2 - x = 0
hay x = -5 hoặc x = 2
d/ 2x2 + 5x - 3 = 0
2x2 - x + 6x - 3 = 0
x(2x-1) + 3(2x-1) = 0
(2x-1).(x+3) = 0
=> 2x-1=0 hoặc x+3=0
hay x = 1/2 hoặc x = -3

a: \(\dfrac{1}{x+2}=\dfrac{2x-x^2}{x\left(2-x\right)\left(2+x\right)}\)
\(\dfrac{8}{2x-x^2}=\dfrac{8}{x\left(2-x\right)}=\dfrac{8x+16}{x\left(2-x\right)\left(2+x\right)}\)
b: \(x^2+1=\dfrac{x^4-1}{x^2-1}\)
\(\dfrac{x^4}{x^2-1}=\dfrac{x^4}{x^2-1}\)
c: \(\dfrac{x^3}{x^3-3x^2y+3xy^2-y^3}=\dfrac{x^3}{\left(x-y\right)^3}=\dfrac{x^3y}{y\cdot\left(x-y\right)^3}\)
\(\dfrac{x}{y^2-xy}=\dfrac{x}{y\left(y-x\right)}=\dfrac{-x}{y\left(x-y\right)}=\dfrac{-x\left(x-y\right)^2}{y\left(x-y\right)^3}\)

?1 . Có . Mẫu thức chung : 12x2y3z đơn giản hơn
?2 . \(\dfrac{3}{x^2-5x}=\dfrac{3}{x\left(x-5\right)}=\dfrac{6}{2x\left(x-5\right)}\)
\(\dfrac{5}{2x-10}=\dfrac{5}{2\left(x-5\right)}=\dfrac{5x}{2x\left(x-5\right)}\)
?3 . \(\dfrac{3}{x^2-5x}=\dfrac{3}{x\left(x-5\right)}=\dfrac{6}{2x\left(x-5\right)}\)
\(\dfrac{-5}{10-2x}=\dfrac{5}{2x-10}=\dfrac{5}{2\left(x-5\right)}=\dfrac{5x}{2x\left(x-5\right)}\)

Bài giải
a) \(\dfrac{1}{x+2}=\dfrac{x.\left(x-2\right)}{\left(x+2\right)\left(x-2\right).x}=\dfrac{x^2-2x}{x\left(x+2\right)\left(x-2\right)}\)
\(\dfrac{8}{2x-x^2}=\dfrac{8}{x\left(2-x\right)}=-\dfrac{8}{x\left(x-2\right)}=-\dfrac{8.\left(x+2\right)}{x\left(x-2\right)\left(x+2\right)}\)
b) \(x^2+1=\dfrac{x^2+1}{1}=\dfrac{\left(x^2+1\right)\left(x^2-1\right)}{x^2-1}=\dfrac{x^4-1}{x^2-1}\)
\(\dfrac{x^4}{x^2-1}\) giữ nguyên.
c) \(\dfrac{x^3}{x^3-3x^2y+3xy^2-y^3}=\dfrac{x^3}{\left(x-y\right)^3}=\dfrac{x^3.y}{\left(x-y\right)^3.y}=\dfrac{x^3y}{y\left(x-y\right)^3}\)
\(\dfrac{x}{y^2-xy}=\dfrac{x}{y.\left(y-x\right)}=-\dfrac{x}{y.\left(x-y\right)}=-\dfrac{x\left(x-y\right)^2}{y.\left(x-y\right).\left(x-y\right)^2}=\dfrac{x\left(x-y\right)^2}{y.\left(x-y\right)^3}\)

Ta có: \(\frac{x^2y+2xy^2+y^3}{2x^2+xy-y^2}\)
\(=\frac{x^2y+xy^2+xy^2+y^3}{2x^2+2xy-xy-y^2}\)
\(=\frac{xy\left(x+y\right)+y^2\left(x+y\right)}{2x\left(x+y\right)-y\left(x+y\right)}\)
\(=\frac{\left(x+y\right)\left(xy+y^2\right)}{\left(2x-y\right)\left(x+y\right)}=\frac{xy+y^2}{2x-y}\left(đpcm\right)\)
Ta có: \(\frac{x^2+3xy+2y^2}{x^3+2x^2y-xy^2-2y^3}\)
\(=\frac{x^2+xy+2xy+2y^2}{x^2\left(x+2y\right)-y^2\left(x+2y\right)}\)
\(=\frac{x\left(x+y\right)+2y\left(x+y\right)}{\left(x^2-y^2\right)\left(x+2y\right)}\)
\(=\frac{\left(x+2y\right)\left(x+y\right)}{\left(x+y\right)\left(x-y\right)\left(x+2y\right)}=\frac{1}{x-y}\left(đpcm\right)\)

Ta có \(\frac{2}{x^3-y^3}=\frac{2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(\frac{2x-1}{x^2-y^2}=\frac{2x+1}{\left(x+y\right)\left(x-y\right)}\)
\(\frac{1}{x+y}\) giữ nguyên
MTC: \(\left(x+y\right)\left(x-y\right)\left(x^2+xy+y^2\right)\)
Các nhân tử phụ tương ứng là : \(\left(x+y\right);\left(x-y\right)\left(x^2+xy+y^2\right);\left(x^2+xy+y^2\right)\)
Ta có:
\(\frac{2}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\frac{2.\left(x+y\right)}{\left(x-y\right)\left(x+y\right)\left(x^2+xy+y^2\right)}\)
\(\frac{1}{x+y}=\frac{1.\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x+y\right)\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(\frac{2x+1}{\left(x+y\right)\left(x-y\right)}=\frac{\left(2x+1\right)\left(x^2+xy+y^2\right)}{\left(x+y\right)\left(x-y\right)\left(x^2+xy+y^2\right)}\)

Bài 1
a) \(\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=x\left(x^2-xy+y^2\right)+y\left(x^2-xy+y^2\right)\)
\(=x^3-x^2y+xy^2+x^2y-xy^2+y^3\)
\(=x^3+y^3\left(Đpcm\right)\)
b) \(\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x\left(x^2+xy+y^2\right)-y\left(x^2+xy+y^2\right)\)
\(=x^3+x^2y+xy^2-x^2y-xy^2-y^3\)
\(=x^3-y^3\left(Đpcm\right)\)
Bài 2
a) \(16x^2-24xy+9y^2\)
\(=\left(4x\right)^2-2.4x.3y+\left(3y\right)^2\)
\(=\left(4x-3y\right)^2\)
b) \(\left(x-2\right)^2-y^2\)
\(=\left(x-2-y\right)\left(x-2+y\right)\)
Bài 3
a) \(\left(x+2\right)\left(x^2-2x+4\right)+x\left(x-5\right)\left(x+5\right)=-17\)
\(\Rightarrow x^3+2^3+x\left(x^2-5^2\right)=-17\)
\(\Rightarrow x^3+8+x^3-25x=-17\)
\(\Rightarrow2x^3-25x=-17-8=-25\)
Hình như câu này đề sai rồi đấy bạn ![]()
b) \(25x^2-2=0\)
\(\Rightarrow25x^2=2\)
\(\Rightarrow x^2=\dfrac{2}{25}\)
\(\Rightarrow\left[{}\begin{matrix}x=\sqrt{\dfrac{2}{25}}\\x=-\sqrt{\dfrac{2}{25}}\end{matrix}\right.\)
1.
\(a.\left(x+y\right).\left(x^2-xy+y^2\right)=x^3-x^2y+xy^2+x^2y-xy^2+y^3=x^3+y^3\)\(b.\left(x-y\right)\left(x^2+xy+y^2\right)=x^3+x^2y+xy^2-x^2y-xy^2-y^3=x^3-y^3\)2.
\(a.16x^2-24xy+9y^2=\left(4x\right)^2-2.4x.3y+\left(3y\right)^2=\left(4x-3y\right)^2\)\(b.\left(x-2\right)^2-y^2=\left(x-2-y\right)\left(x-2+y\right)\)
3.
\(b.25x^2-2=0\)
\(\Leftrightarrow25x^2=2\Leftrightarrow x^2=\dfrac{2}{25}\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{\dfrac{2}{25}}\\x=-\sqrt{\dfrac{2}{25}}\end{matrix}\right.\)