Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu F1=F2
do góc giữa vecto F1, F2=60o
áp dụng định lý hàm cos
F2=F12+ F22+2F1F2cos (vecto)
=> F1=0,58F
|
Phân tích lực F→F→ thành hai lực F1−→F1→ và F2−→F2→ theo hai phương OA và OB (hình 9.10). Giá trị nào sau đây là độ lớn của hai lực thành phần? A. F1 = F2 = F; B. F1 = F2 = 1212F; C. F1 = F2 = 1,15F; D. F1 = F2 = 0,58F. |

Bài 1:
\(\alpha= 0\) \(\Rightarrow F = F_1+F_2 = 16+12=28N\)
\(\alpha = 30^0\)\(\Rightarrow F^2=16^2+12^2+2.16.12.\cos30^0=...\Rightarrow F\)
Các trường hợp khác bạn tự tính nhé.
Bài 2:
Ta có: \(F_1=k.\Delta \ell_1=k.(0,24-0,12)=0,12.k=5\) (1)
\(F_1=k.\Delta \ell_2=k.(\ell-0,12)=10\) (2)
Lấy (2) chia (1) vế với vế: \(\dfrac{\ell-0,12}{0,12}=2\)
\(\Rightarrow \ell = 0,36m = 36cm\)
Bài 3:
Áp lực lên sàn: \(N=P=mg\)
Áp dụng định luật II Niu tơn ta có: \(F=m.a\Rightarrow -F_{ms}=ma\)
\(\Rightarrow a = \dfrac{-F_{ms}}{m}= \dfrac{-\mu.N}{m}== \dfrac{-\mu.mg}{m}=-\mu .g =- 0,1.10=-1\)(m/s2)
Quãng đường vật đi được đến khi dừng lại là \(S\)
Áp dụng công thức độc lập: \(v^2-v_0^2=2.a.S\)
\(\Rightarrow 0^2-10^2=2.1.S\Rightarrow S = 50m\)

chọn hệ trục xOy như hình vẽ ta có
các lực tác dụng lên vật là: \(\overrightarrow{Fms},\overrightarrow{F},\overrightarrow{P},\overrightarrow{N}\)
theo định luật 2 Newton ta có
\(\overrightarrow{F}+\overrightarrow{Fms}+\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{a}.m\left(1\right)\)
chiếu phương trình 1 lên trục Oy ta có
-P + N=0
\(\Leftrightarrow\)P=N\(\Rightarrow\)Fms=\(\mu.N=\mu.mg\)
chiếu pt 1 lên trục Ox ta có
F-Fms=am
\(\Rightarrow\)F=am-Fms=a.m-\(\mu mg\)=1,25.10-0,3.4.10=0,5(N)
Vậy ..........
O x y P N Fms F
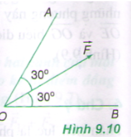
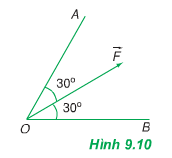

Áp dụng quy tắc hình bình hành: Từ điểm ngọn của vecto F lần lượt vẽ các đoạn song song với hai phương OA và OB ta được các vecto F1 trên OA và F2 trên OB sao cho
Hình bình hành có đường chéo cũng là đường phân giác của 1 góc nên nó là hình thoi.
Suy ra: F1 = F2
Mà