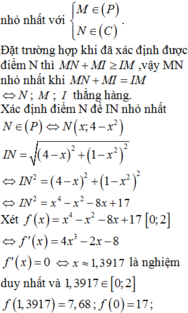Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
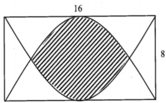
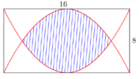
Đặt hai parabol vào trong hệ trục tọa độ Oxy với trục hoành trùng với một cạnh dài và gốc tọa độ O là trung điểm của cạnh dài đó. Từ giả thiết, hai parabol có phương trình lần lượt là
![]()
Phương trình hoành độ giao điểm của hai parabol là

Diện tích trồng hoa được xác định theo công thức
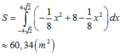
Số tiền cần dùng bằng 2.715.000 đồng

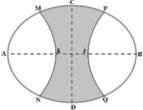
Chọn gốc toạ độ O=AB∩CD, các tia Ox, Oy lần lượt trùng với các tia OB, OC.
Elip có độ dài trục lớn AB=8m, độ dài trục nhỏ CD=6m có phương trình là
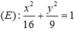
Diện tích của cả hình elip là ![]()
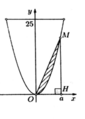
Theo giả thiết có F(1;0) và
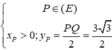
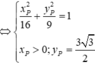
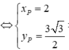
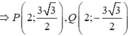
Parabol có trục đối xứng là Ox qua các điểm F, P, Q có dạng ( P ) : x = a y 2 + b y + c
Thay toạ độ các điểm F,P,Q vào phương trình parabol có
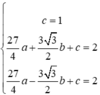

Nửa elip bên phải trục tung là
x
=
4
1
-
y
2
9
. Diện tích hình phẳng giới hạn bởi nửa elip này và parabol (P) là 
Diện tích phần tô đậm bằng
![]()
Số tiền cần dùng
![]()
≈ 4.809.142 đồng
Chọn đáp án D.

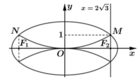
Diện tích Elip: ![]()
Chọn hệ trục tọa độ và gọi các điểm như hình.
Phương trình Elip là: ![]()
Suy ra đường Elip nằm trên trục Ox là: ![]()
Giao điểm của đường thẳng d:
x
=
2
3
đi qua tiêu điểm
F
2
và nửa Elip nằm bên trên trục Ox là ![]()
Parabol đi qua các điểm ![]() có phương trình
có phương trình ![]()
Khi đó diện tích 
Khi đó diện tích
Vậy số tiền cần chi phí: ![]()
Chọn D.

\(\left(C_1\right)\) có dạng \(y=x^3-3x\)
Gọi điểm A(a;2) là điểm kẻ đc 3 tiếp tuyến đến C do đề bài yêu cầu tìm điểm thuộc đường thẳng y=2
ta tính \(y'=3x^2-3\)
gọi \(B\left(x_0;y_0\right)\) là tọa độ tiếp điểm
phương trình tiếp tuyến tại điểm B có dạng
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0\)
suy ra ta có \(y=\left(3x^2_0-3\right)\left(x-x_0\right)+x_0^3-3x_0\)
do tiếp tuyến đi qua điểm A suy ra tọa độ của A thỏa mãn pt tiếp tuyến ta có
\(2=\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0\Leftrightarrow-\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0-2=0\Leftrightarrow-3\left(x_0-1\right)\left(1+x_0\right)\left(a-x_0\right)+\left(1+x_0\right)^2\left(x_0-2\right)=0\)(*)
từ pt * suy ra đc 1 nghiệm \(x_0+1=0\Rightarrow x_0=-1\) hoặc\(-3\left(x_0-1\right)\left(a-x_0\right)+\left(1+x_0\right)\left(x_0-2\right)=0\)(**)
để qua A kẻ đc 3 tiếp tuyến thì pt (*) có 3 nghiệm phân biệt
suy ra pt (**) có 2 nghiệm phân biệt khác -1
từ đó ta suy ra đc a để pt có 2 nghiệm phân biệt khác -1
suy ra đc tập hợ điểm A để thỏa mãn đk bài ra

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

Chọn B.
Phương pháp: Sử dụng phương pháp tọa độ trong mặt phẳng.
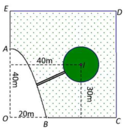
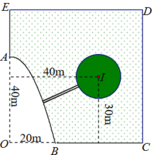
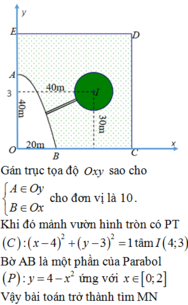
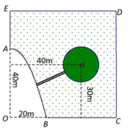
Cách giải: Chọn hệ trục tọa độ Đề các vuông góc như sau:
Gốc O, chiều dương trục hoành là tia OC, chiều dương trục tung là tia OE, đơn vị hai trục là đơn vị độ dài 1m
Khi đó ta có phương trình Parabol là

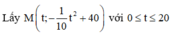
nằm trên Parabol thì khoảng cách ngắn nhất từ đường tròn đến M là
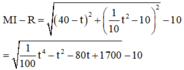
Khảo sát hàm số suy ra khoảng cách ngắn nhất xấp xỉ 17,7