

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
Gọi A là số lượng thành viên ban đầu của đàn ong.
Sau 1 năm, số lượng thành viên trong đàn là ![]()
Sau 2 năm, số lượng thành viên trong đàn là
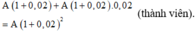
Sau n năm, số lượng thành viên trong đàn là ![]()
Vậy sau 5 năm, số lượng thành viên của đàn ong là
![]()

Đáp án D
Gọi A là số lượng thành viên ban đầu của đàn ong.
Sau 1 năm, số lượng thành viên trong đàn là A + A . 0 , 02 = A 1 + 0 , 02 (thành viên).
Sau 2 năm, số lượng thành viên trong đàn là A 1 + 0 , 02 + A 1 + 0 , 02 . 0 , 02 = A 1 + 0 , 02 2 (thành viên).
….
Sau n năm, số lượng thành viên trong đàn là A 1 + 0 , 02 n (thành viên).
Vậy sau 5 năm, số lượng thành viên của đàn ong là 5 .10 3 1 + 0 .02 5 = 5 .10 3 . 1 , 02 5 (thành viên).

Vận tốc của Dũng là: 12 km / h = 12 000 m / 3600 s = 3,3 m / s
Vận tốc của ong là: 5 m / s
Vậy ong đến B trước.

Đáp án C.
Phương pháp: Sử dụng tổng 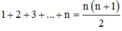
Cách giải: Giả sử trồng được n hàng cây với quy luật trên thì số cây trồng được là:
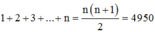
![]()

Câu 1 : Việc gõ ký hiệu như bạn đề cập ; mình cũng không biết phải làm sao nên cứ dùng xyz vậy thôi.
Ta có:
xyz = 100x +10y +z = 111x -11x +10y +z = 37.3x -(11x-10y-z) chia hết cho 37
=> (11x-10y-z) chia hết cho 37
Lại có:
xyz -yzx = 100x +10y +z -100y -10z -x = 99x -90y -9z = 9.(11x-10y-z) chia hết cho 37
Vậy yzx cũng phải chia hết cho 37
Có thể phát biểu hay hơn là CMR: Khi hoán vị các chữ số của 1 số có 3 chữ số chia hết cho 37 thì được số mới cũng chia hết cho 37.

Lời giải:
\(A=a_1a_2+a_2a_3+....+a_{n-1}a_n+a_na_1=0\)
Nếu $n$ lẻ, ta thấy tổng $A$ gồm lẻ số hạng, mỗi số hạng có giá trị $1$ hoặc $-1$ nên $A$ lẻ \(\Rightarrow A\neq 0\) (vô lý)
Do đó $n$ chẵn. Nếu $n$ có dạng $4k+2$. Vì $A=0$ nên trong $4k+2$ số hạng trên sẽ có $2k+1$ số có giá trị là $1$ và $2k+1$ số có giá trị $-1$. Vì mỗi số $a_i$ trong $A$ xuất hiện $2$ lần nên \(a_1a_2a_2a_3....a_{n-1}a_na_{n}a_{1}=(a_1a_2...a_n)^2=1^{2k+1}(-1)^{2k+1}=-1\) (vô lý)
Do đó $n$ phải có dạng $4k$, tức là $n$ chia hết cho $4$ (đpcm)