Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
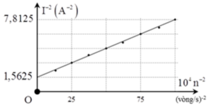
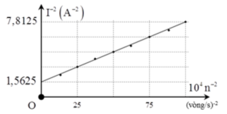
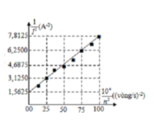
Ta có: I = ω Φ r 2 + ω 2 L 2 ⇒ 1 I 2 = r 2 ω 2 Φ 2 + L 2 Φ 2
Có: f = np; p = 1 => r = 10 Ω ⇒ 1 I 2 = r 2 4 πn 2 Φ 2 + L 2 Φ 2
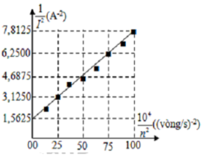
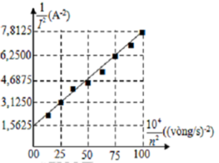
+ 10 4 n 2 = 0 ⇒ 1 n 2 = 0 ⇒ 1 I 0 2 = L 4 Φ 2 = 1 , 5625 (1)
+ 10 4 n 2 = 100 ⇒ 1 n 2 = 0 , 01 ⇒ 1 I 2 = r 2 100 . 4 π 2 Φ 2 + L 4 Φ 2 = 7 , 8125 (2)
( 1 ) ( 2 ) = L 2 r 2 100 . 4 π 2 + L 2 = 1 , 5625 7 , 8125 = 1 5 ⇒ L = 0 , 25 H

Chọn đáp án A
Khi tốc độ quay của động cơ là 1500 vòng/phút thì tần số của dòng điện là f = pn/60 = 50Hz
Khi đó, ta tính được ZL = 200Ω, ZC = 100Ω và R = 100Ω
Và ta tính được tổng trở của mạch Z = 100√2Ω
Điện áp hiệu dụng hai đầu đoạn mạch khi đó là U = IZ = 100 V
+ Khi tốc độ quay của động cơ là n0 thì điện áp hiệu dụng hai đầu tụ điện đạt giá trị cực đại, tần số của dòng điện trong mạch khi đó là f0

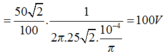

Đáp án A
+ Cường độ dòng điện hiệu dụng qua mạch:
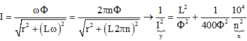
+ Từ đồ thị ta xác định được hai cặp giá trí tương ứng của
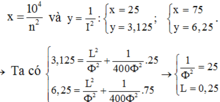

- Cường độ dòng điện hiệu dụng qua mạch:
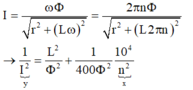
- Từ đồ thị ta xác định được hai cặp giá trí tương ứng của x và y:
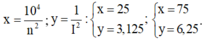
⇒ Ta có hệ:
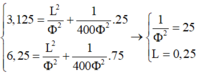

Đáp án A
Phương pháp: Suất điện động hiệu dụng E = ωϕ. Cường độ dòng điện hiệu dụng I = E/Z Tần số của dòng điện xoay chiều f = np (n là tốc độ quay của roto ; p là số cặp cực)
Cách giải:
Ta co: I = ω ϕ r 2 + ω 2 L 2 ⇒ 1 I 2 = r 2 ω 2 ϕ 2 + L 2 ϕ 2 . Có f = np; p = 1
⇒ ω = 2 π n ; r = 10 π
![]()
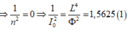
![]()
⇒ L = 0 , 25 H

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V


Dựa vào giản đồ xét tam giác vuông OAB có
\(\sin60=\frac{Uc}{U_{ }AB}\Rightarrow U_C=100.\sin60=50\sqrt{3}V\Rightarrow Z_C=\frac{U_C}{I}=\frac{50\sqrt{3}}{0.5}=100\sqrt{3}\Omega\)
=> \(C=\frac{1}{Z_C.\omega}\)
\(\cos60=\frac{U_R}{U_{AB}}\Rightarrow U_R=50\Omega\Rightarrow R=\frac{U_R}{I}=100\Omega\)
2. Công suất trên mạch có biểu thức
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\\=\frac{U^2}{R^{ }+\frac{\left(Z_L-Z_C\right)^2}{R}}\)
L thay đổi để P max <=> Mẫu Min => áp dụng bất đẳng thức cô-si cho hai số không âm=> \(R=\left|Z_L-Z_C\right|\)
=> \(R=100-40=60\Omega\)
=>
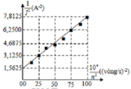
Đáp án A
Ta có:
Có: f = np ; p = 1 => = 2 n ; r = 10 Ω