Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức về độ biến thiên động năng
m v 2 /2 - m v 0 2 /2 = A = - F c s
Trong đó F c là lực cản và s là độ xuyên sâu của viên đạn vào gỗ.
Khi viên đạn xuyên qua tấm gỗ dày s’ = 2 cm và bay ra ngoài, ta tìm được vận tốc của viên đạn khi vừa bay ra khỏi tấm gỗ (với lực cản của gỗ F c không đổi) :
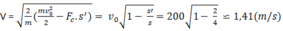

Động năng của viên đạn khi va chạm với tường :
W đ = 1/2.(m v 2 ) = 1/2.(2. 10 - 3 ). 200 2 = 40J
Khi bị bức tường giữ lại, viên đạn đã nhận được công có độ lớn A = W đ
Do viên đạn không trao đổi nhiệt với môi trường bên ngoài nên công A phải bằng độ tăng nội năng của viên đạn :
∆ U = A
Phần nội năng tăng thêm này làm viên đạn nóng lên : Q = mc ∆ t
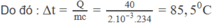

Chọn đáp án A
A = 1 2 m v 2 2 - 1 2 m v 1 2 = - F . s ⇒ F = m 2 s v 1 2 - v 2 2 = 10000 ( N )

Đáp án A .
Theo định lí động năng :
A = 1 2 m v 2 2 − 1 2 m v 1 2 = − F . s ⇒ F = m 2 s v 1 2 − v 2 2 = 10000 N

Độ biến thiên động năng của viên đạn bằng công của lực cản:
\(\dfrac{1}{2}mv-\dfrac{1}{2}mv_0^2=-F_c.s\)
Khi viên đạn xuyên vào gỗ nó dừng lại thì \(v=0\)
\(\Rightarrow-\dfrac{1}{2}mv_0^2=-F_c.s\)
\(\Rightarrow F_c=\dfrac{mv_0^2}{2s}=\dfrac{0,05.200^2}{2.0,04}=25000\) (N)
Nếu viên đạn xuyên qua tấm gỗ dày 2 cm chui ra ngoài thì ta có
\(\dfrac{1}{2}mv'^2-\dfrac{1}{2}mv_0^2=-F_c.s'\)
\(\Rightarrow v'=\sqrt{\dfrac{2}{m}\left(\dfrac{1}{2}mv_0^2-F_c.s'\right)}=\sqrt{v_0^2-\dfrac{2F_c.s'}{m}}=\sqrt{200^2-\dfrac{2.25000.0,02}{0,05}0^2}\approx141\) (m/s)

Năng lượng của viên đạn là: \(\frac{1}{2}mv^2=1000J\)
a. Để vật dừng lại trong gỗ thì năng lượng của vật chuyển hóa hoàn toàn thành công của lực cản:
\(F_c.S_1=E\Rightarrow F_c=250N\)
b.Công của lực cản chính là độ biến thiên năng lượng:
\(\frac{1}{2}mv^2-\frac{1}{2}mv'^2=F_c.S_2\)\(\Rightarrow v'=100\sqrt{2}m\text{/}s\)


Khi bay qua tấm gỗ, viên đạn sinh công A' để thắng công cản của tấm gỗ và chuyển thành nhiệt Q làm nóng viên đạn :
Q = A' (1)
Ta có: A' = m v 1 2 2 - m v 2 2 /2 (2)
Q = mc( t 2 - t 1 ) = mc ∆ t
Từ (1), (2), (3) tính được : ∆ t ≈ 207 ° C.