Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

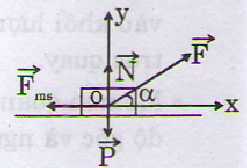
Lực tác dụng lên vật m được biểu diễn trên hình vẽ.
Định luật II Niu-tơn cho:
Chọn hệ trục Oxy với chiều dương là chiều chuyển động theo phương Ox, chiếu phương trình (1) lên:
(Ox): Fcosα- fms= ma (2)
(Oy): N + Fsinα – P = 0 (3)
mà fms= μN (4)
(2), (3) và (4) => F cosα – μ(P- Fsinα ) = ma
=> Fcosα – μP + μFsinα = ma
F(cosα +μsinα) = ma +μmg
=> F =
a) khi a = 1,25 m/s2


chọn hệ trục xOy như hình vẽ ta có
các lực tác dụng lên vật là: \(\overrightarrow{Fms},\overrightarrow{F},\overrightarrow{P},\overrightarrow{N}\)
theo định luật 2 Newton ta có
\(\overrightarrow{F}+\overrightarrow{Fms}+\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{a}.m\left(1\right)\)
chiếu phương trình 1 lên trục Oy ta có
-P + N=0
\(\Leftrightarrow\)P=N\(\Rightarrow\)Fms=\(\mu.N=\mu.mg\)
chiếu pt 1 lên trục Ox ta có
F-Fms=am
\(\Rightarrow\)F=am-Fms=a.m-\(\mu mg\)=1,25.10-0,3.4.10=0,5(N)
Vậy ..........
O x y P N Fms F

Vì vật chuyển động đều
\(\Rightarrow\overrightarrow{F}+\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{F_{ms}}=\overrightarrow{0}\)
Chọn trục toạ độ có trục hoành hướng sang phải, trục tung hướng lên
\(\Rightarrow\left\{{}\begin{matrix}Ox:F.\cos\alpha-F_{ms}=0\\Oy:F.\sin\alpha+N-P=0\end{matrix}\right.\)
\(\Rightarrow F.\cos\alpha-\mu.\left(P-F.\sin\alpha\right)=0\)
\(\Leftrightarrow120.\cos60-\mu.\left(200-120.\sin60\right)=0\)
=> \(\mu=...\)
Tìm gia tốc trong trường hợp alpha= 300 thì lúc này vật chuyển động biến đổi đều nên có gia tốc, tức là \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
Cậu chiếu lên trục toạ độ rồi phân tích, bt hệ số ma sát rồi thì tìm a ez

Đề bài không cho khối lượng nên mình cũng đang thắc mắc . Các bạn giúp mình nha.

O x F Fms P N y
a, Chọn hệ quy chiếu như hình vẽ
Áp dụng định luật 2 newton có: F +N +P +Fms=m.a (1)
chiếu (1) lên Oy: N=P=m.g=0,8.10=8N
chiếu (1) lên Ox:F-Fms=m.a=0,8.a
⇔2-0,2.8=0,8.a
⇔a=0,5(m/s2)
quãng đg vật đi đc sau 2s là: S= \(\dfrac{at^2}{2}\)=1m

giải
Công của trọng lực thực hiện từ lúc vật lên dốc đến lúc dừng lại trên dốc bằng: Ap=mgh
Với h là hiệu độ cao từ vị trí đầu đến vị trí cuối, tính theo hình ta có:

a) theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{N}+\overrightarrow{F_{ms}}+\overrightarrow{P}=m.\overrightarrow{a}\) (1)
chiếu (1) lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
\(cos\alpha.F-\mu.N=m.a\) (2)
chiếu (1) lên trục Oy phương thẳng đứng chiều dương hướng lên trên
N=P-sin\(\alpha\).F (3)
từ (2),(3) và để vật chuyển động với a=0,5
\(\Rightarrow F\approx\)19N
b) sau 3s lực kéo biến mất
theo định luật II niu tơn
\(\overrightarrow{N}+\overrightarrow{F_{ms}}+\overrightarrow{P}=m.\overrightarrow{a'}\) (*)
chiếu (*) lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
\(-\mu.N=m.a'\) (4)
chiếu (*) lên trục Oy phương thẳng đứng chiều dương hướng lên trên
\(N=P-sin\alpha\) (5)
từ (4),(5)
\(\Rightarrow a'\approx-2,46\)m/s2
ngay sau khi lực F biến mất vận tốc vật lúc đó là
v=a.t=1,5m/s2
thời gian vật đi được đến khi dừng kể từ lúc lực F biến mất
t=\(\dfrac{v_1-v}{a'}\approx0,6s\)

\(\overrightarrow{F_{ht}}=m.\overrightarrow{a_{ht}}\Rightarrow F_{ht}=m.a_{ht}\)
\(\overrightarrow{F_{msn}}=\mu.\overrightarrow{N}\Rightarrow F_{msn}=\mu mg\)
Có \(F_{ht}\le F_{msn}\Rightarrow m.a_{ht}\le\mu mg\)
\(\Leftrightarrow\omega^2.R\le\pi^2.\mu\)
\(\Leftrightarrow\pi^2.0,2\le\pi^2.\mu\Rightarrow\mu\ge0,2\)
Vậy để vât ko bị trượt thì \(\mu\ge0,2\)


Chọn đáp án D
Lực tác dụng vào vật
+ Lực kéo động cơ F
+ Lực ma sát Fms
+ Trọng lực P
+ Phản lực của mặt sàn N
Theo định luật II Newton: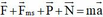 (1)
(1)
Chọn hệ trục tọa độ xOy như hình vẽ
Chiếu (1) lên trục Oy: F sin 30 0 + N − P = 0 (2)
Chiếu (1) lên trục Ox: F cos 30 0 − Fms = ma (3)
Từ (2) → N = mg = −F sin 30 0
→ Fms= µN = P (mg − Fsin 30 0 ) (4)
Thế (4) vào (3), ta được: F cos 30 0 − µ(mg − Fsin 30 0 ) = ma (5)
Khi vật chuyển động với gia tốc a
+ Từ (5):
+ Với