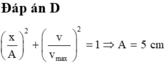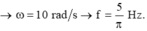Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức độc lập, ta có: \(A^2 = x^2+\frac{v^2}{\omega^2} \Rightarrow\) \(8^2+\frac{12^2}{\omega^2} = 6^2+\frac{16^2}{\omega^2} \Rightarrow \omega = 2 \ (rad/s) \Rightarrow f = \frac{1}{\pi} \ Hz\)

Áp dụng:
+ \(A^2 = x^2 + \frac{v^2}{\omega^2} = 3^2+\frac{40^2}{\omega^2}\) (1)
+ Qua VTCB, vận tốc cực đại: \(v_{max} = \omega A \Rightarrow 50 = \omega A\) (2)
Từ (1) và (2) \(\Rightarrow \omega = 10 \ (rad/s); A = 5 \ cm\)
+ Khi vận tốc đạt giá trị v3 = 30cm/s, ta có: \(x = \pm\sqrt{A^2-\frac{v^2}{\omega^2}} = \pm 4 \ cm\)

Làm tương tự bài này Câu hỏi của Nguyễn Lê Quỳnh Anh - Vật lý lớp 12 | Học trực tuyến

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

Áp dụng công thức: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2=2,5^2+\dfrac{(50\sqrt 3)^2}{\omega^2}=(2,5\sqrt 3)^2+\dfrac{50^2}{\omega^2}\)
\(\Rightarrow \omega = 20(rad/s)\)
Và \(A=5cm\)

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)