Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega=2\pi f = 9\pi (rad/s)\)
Biên độ \(A=(56-40)/2=8(cm)\)
Gốc thời gian lúc lò xo ngắn nhất --> biên độ (-A) -->\(\varphi=-\pi (rad)\)
Vậy: \(x=8\cos(9\pi t-\pi)(cm)\)
Chọn D.

\(\Delta l=5cm\)
Vị trí có lực đẩy đàn hồi lần thứ nhất chính là vị trí lò xo bắt đầu bị nén. Tức là qua vị trí -\(x=-\Delta l\).
M -10 10 N -5 ^
Vị trí ban đầu t = 0 tại M ứng với góc (-90 độ).
Vị trí lực đầy đàn hồi lần thứ nhất tại N x = -5 cm.
=> \(\varphi=\pi+\frac{\pi}{6}=\frac{7\pi}{6}\Rightarrow t=\frac{\varphi}{\omega}=\frac{7\pi}{6.10\pi}=\frac{7}{60}s.\)
sai rồi bạn ơi, lực đẩy max là lúc vật ở vị trí -A nhé, denta phi sẽ là 3π/2, và t sẽ là 3/20s

Ban đầu t = 0 thì x = 2 cm, lúc này vật đang ở biên độ dương.
Quả cầu dao động được nửa chu kì thì x = -2 cm (vật ở biên độ âm)
Chiều dài của lò xo: \(\ell=\ell_0+\Delta\ell_0+x=40+10-2=48(cm)\)

\(\Delta l=\frac{g}{\omega^2}=0,25m\)
\(t=0\Rightarrow x=5\sqrt{3}cm\Rightarrow l=l_0+\Delta l+x=158,66cm\)
Vậy không phương án đúng



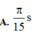
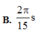
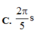
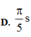
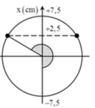

Đáp án B