Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


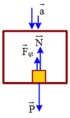
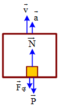
Khi lực nén của người lên sàn thang máy bằng không (N = 0), ta được: F → q t + P → = 0 → ⇒ F → q t ↑ ↓ P → 3 F q t = P 4
(3) suy ra: Thang máy đi xuống nhanh dần đều hoặc thang máy đi lên chậm dần đều
(4) → m | a | = m g → | a | = g = 10 m / s 2
Lực nén của ngvrời lên sàn thang máy bằng không khi thang máy rơi tự do hay thang máy đi lên chậm dần đều với gia tốc bằng g

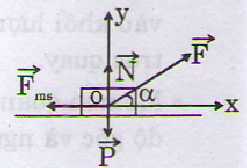
chọn hệ trục xOy như hình vẽ ta có
các lực tác dụng lên vật là: \(\overrightarrow{Fms},\overrightarrow{F},\overrightarrow{P},\overrightarrow{N}\)
theo định luật 2 Newton ta có
\(\overrightarrow{F}+\overrightarrow{Fms}+\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{a}.m\left(1\right)\)
chiếu phương trình 1 lên trục Oy ta có
-P + N=0
\(\Leftrightarrow\)P=N\(\Rightarrow\)Fms=\(\mu.N=\mu.mg\)
chiếu pt 1 lên trục Ox ta có
F-Fms=am
\(\Rightarrow\)F=am-Fms=a.m-\(\mu mg\)=1,25.10-0,3.4.10=0,5(N)
Vậy ..........
O x y P N Fms F

45 P N F dh
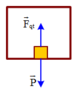
Chọn trục toạ độ như hình vẽ.
Vật ở VTCB lò xo bị nén \(\Delta \ell_0\)
Vật đang đứng yên ở VTCB, hợp lực tác dụng lên vật bằng 0
\(\Rightarrow \vec{P}+\vec{F_{dh}}+\vec{N}=\vec{0}\)
Chiếu lên trục toạ độ ta được: \(P.\sin 45^0-F_{dh}=0\)
\(\Rightarrow mg.\sin 45^0=k.\Delta \ell_0\)
\(\Rightarrow k=\dfrac{mg.\sin 45^0}{\Delta \ell_0}=\dfrac{0,2.10.\sin 45^0}{0,02}=50\sqrt 2(N/m)\)
Chọn C.

giải
Công của trọng lực thực hiện từ lúc vật lên dốc đến lúc dừng lại trên dốc bằng: Ap=mgh
Với h là hiệu độ cao từ vị trí đầu đến vị trí cuối, tính theo hình ta có:

a) theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{N}+\overrightarrow{F_{ms}}+\overrightarrow{P}=m.\overrightarrow{a}\) (1)
chiếu (1) lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
\(cos\alpha.F-\mu.N=m.a\) (2)
chiếu (1) lên trục Oy phương thẳng đứng chiều dương hướng lên trên
N=P-sin\(\alpha\).F (3)
từ (2),(3) và để vật chuyển động với a=0,5
\(\Rightarrow F\approx\)19N
b) sau 3s lực kéo biến mất
theo định luật II niu tơn
\(\overrightarrow{N}+\overrightarrow{F_{ms}}+\overrightarrow{P}=m.\overrightarrow{a'}\) (*)
chiếu (*) lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
\(-\mu.N=m.a'\) (4)
chiếu (*) lên trục Oy phương thẳng đứng chiều dương hướng lên trên
\(N=P-sin\alpha\) (5)
từ (4),(5)
\(\Rightarrow a'\approx-2,46\)m/s2
ngay sau khi lực F biến mất vận tốc vật lúc đó là
v=a.t=1,5m/s2
thời gian vật đi được đến khi dừng kể từ lúc lực F biến mất
t=\(\dfrac{v_1-v}{a'}\approx0,6s\)

Lực tác dụng lên vật m được biểu diễn trên hình vẽ.
Định luật II Niu-tơn cho:
Chọn hệ trục Oxy với chiều dương là chiều chuyển động theo phương Ox, chiếu phương trình (1) lên:
(Ox): Fcosα- fms= ma (2)
(Oy): N + Fsinα – P = 0 (3)
mà fms= μN (4)
(2), (3) và (4) => F cosα – μ(P- Fsinα ) = ma
=> Fcosα – μP + μFsinα = ma
F(cosα +μsinα) = ma +μmg
=> F =
a) khi a = 1,25 m/s2