
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Toa xe trượt không ma sát trên đường dốc với góc nghiêng \(\alpha\)
Ta có kết quả:
+ Khi vật ở VTCB thì phương của sợi dây vuông góc với mặt phẳng nghiêng.
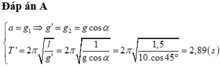
+ Gia tốc hiệu dụng của vật: \(g'=g.\cos a\)
Chu kì dao động: \(T=2\pi\sqrt{\frac{l}{g'}}=2\pi\sqrt{\frac{1,5}{10.\cos45^o}}\approx2,89\left(s\right)\)

Toa xe trượt không ma sát trên đường dốc với góc nghiêng \(\alpha\)
Ta có kết quả:
+ Khi vật ở VTCB thì phương của sợi dây vuông góc với mặt phẳng nghiêng.
+ Gia tốc hiệu dụng của vật: \(g'=g.\cos\alpha\)
Chu kì dao động: \(T=2\pi\sqrt{\dfrac{\ell}{g'}}=2\pi\sqrt{\dfrac{1,5}{10.\cos 45^0}}\approx2,89(s)\)

\(\overrightarrow {g'} =\overrightarrow g - \overrightarrow a \)
Ô tô chuyển động nằm ngang => \(\overrightarrow a \bot \overrightarrow g\)
=> \(g' = \sqrt{g^2+ a^2}\)
\(T = 2\pi \sqrt{\frac{l}{g}}\)
\(T' = 2\pi \sqrt{\frac{l}{g'}}\)
=> \(\frac{T}{T'} = \sqrt{\frac{g'}{g}} = \sqrt{\frac{\sqrt{g^2+a^2}}{g}} = 1,01\)
=> \(T'= \frac{2}{1,01} = 1,98 s.\)
cho mình hỏi: Nếu trong trường hợp ôtô chuyển động thẳng chậm dần đều thì phải làm ntn ?

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

Đáp án B
Trước hết ta tìm gia tốc a chuyển động của toa xe trên mặt phẳng nghiêng
Theo định luật II Niu-tơn :
Xét theo phương Oy vuông góc với mặt phẳng nghiêng :
Phản lực : N = mgcos α
Lực ma sát F = μ N = μ m g cos α
Xét theo phương Ox của mặt phẳng nghiêng thì :
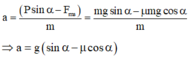
Với β = 90 0 - α ⇒ cos β = sin α , với F = ma
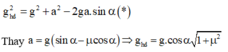
Chu kì dao động bé của con lắc đơn : T = 2 π 1 g hd = 2 π 1 gcosα 1 + μ 2
Từ những dữ kiện trên ta thay số vào tính được : v m a x = 0 , 21 m / s

Vật thực hiện 10 dao động mất 20s:
\(T=\frac{t}{n}=2s\Rightarrow g=4\pi^2\frac{l}{T^2}=9,86m/s^2\)
Đáp án C