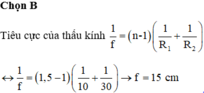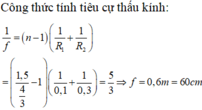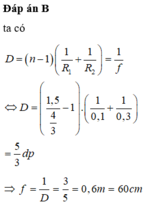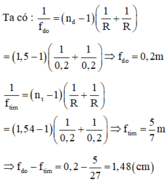Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\)

Tiêu cự của thấu kính được tính bằng công thức
\(\frac{1}{f}=\left(n-1\right)\left(\frac{1}{R_1}+\frac{1}{R_2}\right)\)
Từ đó tính được
\(f_{đỏ=0,2m=20cm}\)
\(f_{tím}\approx18,52\)
Khoảng cách sẽ là:
\(\text{Δd=Δf=1,48cm}\)
----> chọn D

H S I i i gh 20cm
Để mắt người quan sát ở mặt nước không thấy vật sáng ở đáy chậu thì không có tia sáng nào từ vật S thoát ra ngoài, như vậy ít nhất tia tới SI cho tia khúc xạ là là mặt nước như hình vẽ, khi đó góc \(i=i_{gh}\)
=> \(\sin i = \sin i_{gh}=\frac{1}{n}=\frac{3}{4}\)
=>\(\tan i = \frac{3}{\sqrt 7}\)
Mà \(\tan i = \frac{HI}{HS}\Rightarrow HS = HI/\tan i = 20/\frac{3}{\sqrt 7}=\frac{20\sqrt 7}{3}\)cm.
Vậy chiều sâu của nước trong chậu là HS = \(\frac{20\sqrt 7}{3}\)cm.

Đáp án A
Thấu kính hai mặt lõm trong không khí là thấu kính phân kì:
Ta có
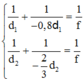
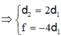
Mặt khác
![]()
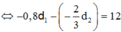

![]()
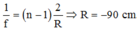

Đáp án A
+ Áp dụng công thức của thấu kính mỏng với hai ánh sang đỏ và tím, ta có:
D d = n d - 1 = 2 R = 1 , 60 - 1 2 R D t = n t - 1 = 2 R = 1 , 69 - 1 2 R .
+ Gọi D là độ tụ của hệ thấu kính khi ghép đồng trục hai thấu kính với nhau (bằng nhua với cả ánh sang đỏ và tím) n ' t , n ' d lần lượt là chiết suất của ánh sang tím và đỏ với thấu kính phân kì.
D = D t + D ' t = 1 , 69 - 1 2 R + n ' t - 1 2 - R D = D d + D ' d = 1 , 60 - 1 2 R + n ' d - 1 2 - R ⇒ n ' t - n ' d = 1 , 69 - 1 , 60 = 0 , 09 .