Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : F = k△l = \(\frac{E.S}{l_0}\). | △l |
→ \(\frac{\triangle l}{l_0}=\frac{F}{E.S}=\frac{157.10^3}{2.10^{11}.\left(10^{-2}\right)^2.3,14}=25.10^{-4}=0,25.10^{-2}\)
Vậy độ biến dạng tỉ đối của thanh là \(\frac{\triangle l}{l_0}=0,25.10^{-2}\)
@phynit
Em trả lời 100% . Không có sự tự hỏi tự trả lời đâu ạ ( Em nói để thầy biết và không nghĩ oan cho em )

Ta có : F = k\(\triangle\)l = \(\frac{E.S}{l_o}\). | \(\triangle\)l |
→ \(\frac{\triangle l}{l_0}=\frac{F}{E.S}=\frac{157.10^3}{2.10^{11}.\left(10^{-2}\right)^2.3,14}\)= 25 . 10-4 = 0,25 .10-2
Vậy độ biến dạng tỉ đối của thanh là \(\frac{\triangle l}{l_0}\)= 0,25 . 10-2

d = 20 mm
E = 2.1011 Pa
Fnén = 1,57.105 N
Tìm \(\varepsilon=\dfrac{\left|\Delta t\right|}{l_0}=?\)
Ta có: \(F=k\Delta l=\dfrac{ES}{l_0}\left|\Delta t\right|\)
\(\Rightarrow\dfrac{\Delta l}{l_0}=\dfrac{F}{ES}=25.10^4=0,25.10^{-2}\)
Vậy độ biến dạng tỉ đối của thanh là : \(\dfrac{\left|\Delta l\right|}{l_0}=2,5.10^{-3}\)

Độ nở dài tỉ đối của :
- Thanh thép khi bị nung nóng từ nhiệt độ t 1 đến t 2 :
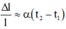
- Thanh thép khi bị biến dạng kéo tính theo định luật Húc :
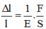
So sánh hai công thức này, ta tìm được lực do thanh thép tác dụng lên hai bức tường nếu nó bị nung nóng từ t 1 = 20 ° C đến t 2 = 200 ° C tính bằng :
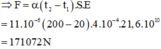

d = 20 mm = 20.10-3m
E = 2.1011 Pa
Fnén = 1,57.105 N
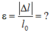
Ta có: 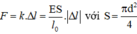
→ Độ biến dạng tỉ đối của thanh:
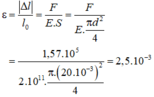

Vì hai bức tường cố định nên khoảng cách giữa chúng không đổi. Khi nhiệt độ tăng thì thanh xà nở dài thêm một đoạn ∆ l = 1,2 mm. Do đó, thanh xà tác dụng lên hai bức tường một lực có cường độ tính theo định luật Húc :
![]()

Chọn D
Lực nén vào thanh thép bằng đúng lực đàn hồi xuất hiện trong thanh.
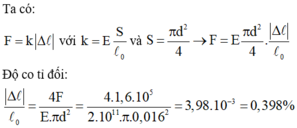

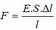
Ta có, lực kéo đàn hồi cần tác dụng lên đầu kia của thanh thép để thanh dài thêm 2,5 mm là: F d h = k . ∆ l = E S l 0 ∆ l = 2 . 10 11 1 , 5 . 10 - 4 5 2 , 5 . 10 - 3 = 15000 N
Đáp án: B