Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C 100m 150m
+ Khi nguồn âm công suất P đặt tại A thì: LB=100dB=L,
Do vậy, nếu nguồn âm công suất P đặt tại B thì tại A có: LA = L = 100 dB.
+ Nếu nguồn âm công suất 2P đặt tại B thì cường độ âm tại A sẽ tăng gấp đôi. Áp dụng: \(L_A'-L_A=10lg\frac{I_A'}{I_A}=10lg2\) \(\Rightarrow L_A'=L_A+10lg2=100+10lg2=103dB\)
Áp dụng: \(_{L_A'-L_C'=20lg\frac{150}{100}}\)\(\Rightarrow L_C'=L_A'-20lg\frac{3}{2}=103-20lg\frac{3}{2}=101dB\)

Đáp án C
Phương pháp: Công thức tính mức cường độ âm:
L = 10 log I I 0 = 10 log P 4 πR 2 I 0
Cách giải:
+ Lúc đầu, mức cường độ âm tại M:
L M = 10 log P 4 πR 2 I 0 = 50 dB
+ Sau khi tăng công suất của nguồn âm lên 30:
L M ' = 10 log P + 0 , 3 P 4 πR 2 I 0 = 10 log 1 , 3 + 10 log P 4 πR 2 I 0 = 1 , 14 + 50 = 51 , 14 dB .

\(\lambda = v/f=20/50=0.4cm.\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{4,8-5,3}{0,4}-\frac{0}{2\pi})|=|2a\cos\frac{-5\pi}{4}|=\sqrt{2}a = 2\sqrt{2}\)
\( u_M = A_M\cos(2\pi ft - \pi\frac{d_2+d_1}{\lambda}+\frac{\varphi_1+\varphi_2}{2})=2\sqrt{2}\cos(40 \pi t - \pi\frac{5,3+4,8}{0,4}+\frac{0}{2}) = 2\sqrt{2}\cos(40 \pi t - \pi\frac{5,3+4,8}{0,4})\\ = 2\sqrt{2}\cos(40 \pi t - 25,25\pi)mm.\)

Biên độ sóng tại một điểm M bất kì cách nguồn O1, O2 lần lượt các đoạn d1, d2 là
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}+\frac{\triangle\varphi}{2\pi})|\)
\(\triangle\varphi = 0\)
Biên độ tại điểm có cực đại giao thoa \(A_{Mmax} = A_0=> 2a =2cm.\)
Để biên độ sóng tại M
\(A_M = 1,2 cm=> |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = 1,2\)
=> \(\cos \pi(\frac{d_2-d_1}{\lambda})= 0,6.\)
\(=> \pi.(\frac{d_2-d_1}{\lambda}) = \frac{53}{180}.\pi+k2\pi\)
=> \(d_2-d_1 = (2k + 0,29)\lambda\ \ (1).\)
M nằm trên đoạn thẳng \(O_1O_2\) tức là (không được tính hai nguồn)
\(-O_1O_2 < d_2-d_1 < O_1O_2\)
Thay (1) vào ta được
\(-O_1O_2 < (2k+0,29)\lambda < O_1O_2\)
=> \(-1,745 < k < 1,455\)
=> \(k = -1,0,1.\)

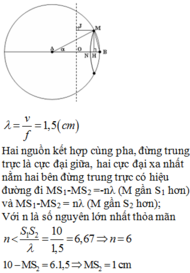
Gọi H là đường chân cao hạ từ O đến MN
Giả sử OH = 1 → OM \(=\sqrt[4]{10};ON=\sqrt{10}\)
Do đó tính \(\widehat{MON}\approx1270,35^o\)
A đúng
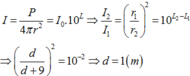
Chọn đáp án D