Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Mức cường độ âm tại M: L M = 10 log I M I 0 ( d B ) = 10 log 10 - 8 10 - 12 = 40 ( d B )

A B C 100m 150m
+ Khi nguồn âm công suất P đặt tại A thì: LB=100dB=L,
Do vậy, nếu nguồn âm công suất P đặt tại B thì tại A có: LA = L = 100 dB.
+ Nếu nguồn âm công suất 2P đặt tại B thì cường độ âm tại A sẽ tăng gấp đôi. Áp dụng: \(L_A'-L_A=10lg\frac{I_A'}{I_A}=10lg2\) \(\Rightarrow L_A'=L_A+10lg2=100+10lg2=103dB\)
Áp dụng: \(_{L_A'-L_C'=20lg\frac{150}{100}}\)\(\Rightarrow L_C'=L_A'-20lg\frac{3}{2}=103-20lg\frac{3}{2}=101dB\)

Đáp án C
Phương pháp: Công thức tính mức cường độ âm:
L = 10 log I I 0 = 10 log P 4 πR 2 I 0
Cách giải:
+ Lúc đầu, mức cường độ âm tại M:
L M = 10 log P 4 πR 2 I 0 = 50 dB
+ Sau khi tăng công suất của nguồn âm lên 30:
L M ' = 10 log P + 0 , 3 P 4 πR 2 I 0 = 10 log 1 , 3 + 10 log P 4 πR 2 I 0 = 1 , 14 + 50 = 51 , 14 dB .

Do E và B biến thiên cùng pha nên, khi cảm ứng từ có độ lớn B0/2 thì điện trường E cũng có độ lớn E0/2.
Bài toán trở thành tính thời gian ngắn nhất để cường độ điện trường có độ lớn E0/2 đang tăng đến độ lớn E0/2.
E M N Eo Eo/2
Từ giản đồ véc tơ quay ta dễ dang tính được thời gian đó là t = T/3
Suy ra: \(t=\dfrac{5}{3}.10^{-7}\)s

Cứ giữa 2 bụng liên tiếp có 2 điểm dao động biên độ 2√⇒ 20 điểm thì k=10
Vậy λ=2cm

Theo công thức liên hệ chiều dài day và số bụng sóng ta có $2,4=8.\dfrac{\lambda}{2} \Rightarrow \lambda =0,6m=60 cm$
Công thức tính biên độ tại một điểm bất kì trên sợi dây cách nút gần nhất một khoảng là d đang có sóng dừng với biên độ tại bụng là 2A:
$a=2A \cos \left(\dfrac{2 \pi d}{\lambda} +\dfrac{\pi }{2} \right).$
Gọi khoảng cách từ A tới nút gần nhất là d thì do $\dfrac{\lambda}{4}<20$ nên ta có B cách nút gần nhất với nó một khoảng 10-d.
$| a_A-a_B |=2A |\left(\dfrac{2 \pi d}{\lambda} +\dfrac{\pi }{2} \right)-\left(\dfrac{2 \pi \left(10-d\right)}{\lambda} +\dfrac{\pi }{2} \right) |$
$=4A |\sin \left(\dfrac{10 \pi }{\lambda}+\dfrac{\pi }{2} \right) | |\sin \left(\dfrac{\pi \left(2x-10\right)}{\lambda}\right) |.$
Biểu thức trên lớn nhất khi $|\sin \left(\dfrac{\pi \left(2x-10\right)}{\lambda}\right) |$ lớn nhất, tức là bằng 1.
Thay số ta có đáp án D
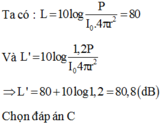
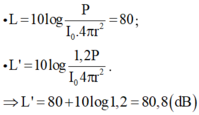
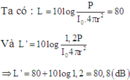
Đáp án D
Phương pháp: Sử dụng công thức tính mức cường độ âm L = 10 log I I 0
Cách giải:
+ Mức cường độ âm tại 1 điểm cách nguồn một khoảng r là: L = 10log I I 0 = 10 log P 4 π r 2 I 0
+ Để máy thu đặt tại một điểm trên đoạn MN thu được mức cường độ âm lớn nhất thì khoảng cách từ nguồn O đến điểm đó phải nh nhất => điểm đó là điểm H H là chân đường cao hạ từ O xuống MN .
+ Gọi độ dài các cạnh của ∆ O M N là a.
Áp dụng định lí Pi – ta – go trong tam giác vuông OMH ta có: OH = a 3 2
+ Mức cường độ âm tại M và H:
L M = 10 log P 4 π . O M 2 . I 0 L H = 10 log P 4 π . O H 2 . I 0
⇒ L H - L M = 20 log O M O H = 20 log a a 3 2 = 1 , 25 ⇒ L H = L M + 1 , 25 = 24 , 77 + 1 , 25 = 26 d B