Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có hình vẽ
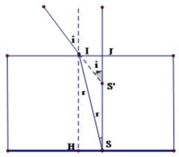
Từ hình vẽ ta thấy rằng IJ = JS’.tani; IJ = JS.tanr
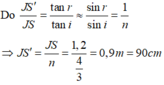

Chọn đáp án B.
Ánh sáng mặt trời chiếu qua mặt nước đập vào viên sỏi, phản xạ, lên rồi khúc xạ ra ngoài không khí. Nếu để mắt hứng các tia khúc xạ thì nhìn thấy ảnh ảo của viên sỏi ở dưới mặt nước (mặt nước đóng vai trò lưỡng chất phẳng nước-không khí). Vì mắt đồng thời nhận được hai chùm sáng phản xạ và khúc xạ trùng nhau nên có cảm giác như viên sỏi được nâng lên gần với mặt nước.
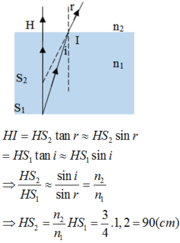

Đáp án A
Ánh sáng mặt trời chiếu qua mặt nước đập vào viên sỏi, phản xạ, lên rồi khúc xạ ra ngoài không khí. Nếu để mắt hứng các tia khúc xạ thì nhìn thấy ảnh ảo của viên sỏi ở dưới mặt nước (mặt nước đóng vai trò lưỡng chất phẳng nước-không khí). Vì mắt đồng thời nhận được hai chùm sáng phản xạ và khúc xạ trùng nhau nên có cảm giác như viên sỏi được nâng lên gần với mặt nước.
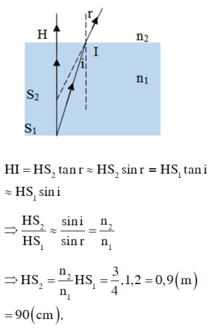

H S I i i gh 20cm
Để mắt người quan sát ở mặt nước không thấy vật sáng ở đáy chậu thì không có tia sáng nào từ vật S thoát ra ngoài, như vậy ít nhất tia tới SI cho tia khúc xạ là là mặt nước như hình vẽ, khi đó góc \(i=i_{gh}\)
=> \(\sin i = \sin i_{gh}=\frac{1}{n}=\frac{3}{4}\)
=>\(\tan i = \frac{3}{\sqrt 7}\)
Mà \(\tan i = \frac{HI}{HS}\Rightarrow HS = HI/\tan i = 20/\frac{3}{\sqrt 7}=\frac{20\sqrt 7}{3}\)cm.
Vậy chiều sâu của nước trong chậu là HS = \(\frac{20\sqrt 7}{3}\)cm.

- Khối lượng nước bị bay hơi mà không ngưng tụ lại trên nước đá là: \(\Delta m = m_0+m-m_1\)
- Nhiệt lượng cần cung cấp để làm lượng nước trên bay hơi là: \(Q_1=\Delta m. L=(m_0+m-m_1).L\)
- Nhiệt lượng cần cung cấp để làm tan đá là: \(Q_2=m.\lambda\)
- Nhiệt lượng cần cung cấp để m gam nước tăng nhiệt đến nhiệt độ sôi là: \(Q_3=m.c.t_s\)
Vậy nhiệt lượng mà bếp cung cấp cho bình nước là: \(Q=Q_1+Q_2+Q_3=(m_0+m-m_1).L+m.\lambda+m.c.t_s\)
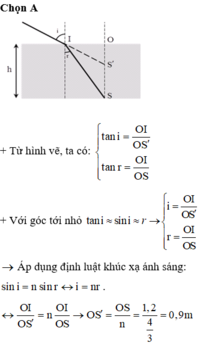
Chọn C
Xét chùm tia tới tới mặt nước gần như vuông góc với mặt nước khi đó góc tới i nhỏ dẫn đến sini gần bằng tani