Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Người lái xuồng dự định đi từ A - B nhưng do nước chảy nên đến C với BC = 180 m.
Quãng đường AC thực tế xuồng đi là


Chọn A.
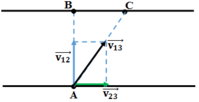
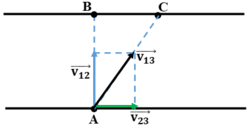
Gọi xuồng là vật 1; nước là vật 2; bờ là vật 3.
V 12 → là vận tốc của xuồng so với nước và v12 = AB/t = 240/60 = 4m/s
V 23 → là vận tốc của nước so với bờ, v23 = BC/t = 180/60 = 3m/s
V 13 → là vận tốc của xuồng so với bờ.
Ta có: V 13 → = V 23 → + V 12 →
Từ hình vẽ ta có:
![]()
Vậy vận tốc xuồng đối với bờ là v13 = 5 m/s.

gọi AB là độ rộng của sông
BC là khoảng từ vị trí dự định đến vị trí thức tế bên kia sông
ta có AC2=AB2+BC2
\(\Rightarrow\)AC=300m
vận tốc thuyền so vơi bờ là
vt,b=300/60=5m/s

sAB = 320m
sBC = 240m
tAC = 100s
A B C 320m 240m 100s
\(\Delta ABC\) vuông tại B, theo định lý pitago ta có:
\(AC^2=AB^2+BC^2=320^2+240^2=160000\)
\(\Rightarrow AC=\sqrt{160000}=400m\)
Vận tốc của xuồng so với dòng sông:
\(v_{xuồng}=\frac{s_{AC}}{t_{AC}}=\frac{400}{100}=4\)m/s

Tóm tắt:
\(S_{AB}=320m\)
\(S_{BC}=240m\)
\(t_{AC}=100s\)
\(v_{xuồng}+v_{nước}=?\)
----------------------------------------------
Bài làm:
A B C 100s 320m 240m
Áp dụng định lí Py-ta-go vào \(\Delta vABC\) ta có:
\(AC^2=AB^2+BC^2\)
\(\Rightarrow AC^2=320^2+240^2=160000\)
\(\Rightarrow AC=\sqrt{160000}=400\left(m\right)\)
Vận tốc của xuồng so với dòng sông là:
\(v_{xuồng}=\dfrac{S_{AC}}{t_{AC}}=\dfrac{400}{100}=4\left(m\text{/}s\right)\)
Vậy vận tốc của xuồng so với dòng sông là:4m/s
Trịnh Công Mạnh Đồng mk nhớ vận tốc xuống so với bờ mới dùng công thức S/t mà bạn

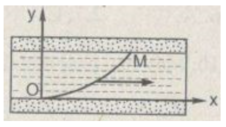
Khi xuồng chạy từ bờ này sang bờ kia thì quỹ đạo của nó là một đường cong, vì xuồng có thể chạy lúc nhanh, lúc chậm và nước có chỗ chảy xiết, có chỗ không, do đó ta nên chọn
- Một vật mốc O gắn cố định với bờ sông
- Hai trục tọa độ vuông góc Ox và Oy: Trục Ox nằm dọc bờ sông, trục Oy nằm vuông góc với bờ sông

Chọn A