

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Thể tích của một viên bi là V 0 = 4 πr 3 3 = 32 π 3 ( c m 3 )
Thể tích nước tăng lên khi bỏ một viên bi vào là V = 85 % V 0 = 136 π 15
Thể tích nước tăng lên là V ' = π 10 2 2 12 - 10 = 50 π cm 3
Vậy V ' V ≈ 5 , 14 nên ít nhất cần 6 viên bi để thỏa mãn đề bài

Đáp án C.
Gọi R 1 = r là bán kính đường tròn đáy của hình nón và cũng là bán kính mặt đáy của thùng.
Khi đó R 2 = 2 r là bán kính của miệng thùng và phễu, thùng có cùng chiều cao h = 20 cm.
Thể tích của thùng là V 1 = 1 3 πh R 1 2 + R 2 2 + R 1 R 2 = 1 2 . π . 20 . r 2 + 4 r 2 + r . 2 r = 140 π 3 . r 2 cm 3 .
Thẻ tích của phễu hình nón là V 2 = 1 3 πR 1 2 h = 1 3 . π . r 2 . 20 = 20 π 3 . r 2 cm 3 .
Vậy thể tích khối nước là V = V 1 - V 2 = 40 πr 2 = 4000 ⇒ r = 100 π ≈ 5 , 64 cm .

Đáp án D.
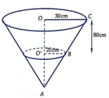
Xét hình nón đỉnh A, đường cao h(h > 80cm) và có đáy là đường tròn tâm O, bán kính R = 30cm. Mặt phẳng cách mặt đáy 80 cm và cắt hình nón theo giao tuyến là đường tròn tâm O' có bán kính r = 20cm. Mặt phẳng chia hình nón thành 2 phần. Phần (I) là phần chứa đỉnh A, phần (II) là phần không chứa đỉnh A (hình vẽ).
Ta có O ' B O C = A O ' A O ⇔ A O ' A O ' + O ' O = 2 3 ⇔ A O ' A O ' + 80 = 2 3 ⇔ A O ' = 160 ( c m )
Thể tích hình nón là V = 1 3 A O . πR 2 = 1 3 160 + 80 . π . 30 2 = 72000 π ( cm 3 )
Thể tích phần (I) là V I = 1 3 A O ' . πr 2 = 1 3 160 π . 20 2 = 64000 3 π ( cm 3 )
Thể tích cái xô cũng là thể tích phần (II), ta có :
V ( I I ) = V - V ( I ) = 72000 π - 64000 3 π = 152000 3 π ( cm 3 ) = 19 375 π ( m 3 )
Vậy số tiền phải trả mỗi tháng là
20000 . V I I . 10 = 20000 . 19 375 π . 10 ≈ 31835 (đồng).

Chọn B.
Phương pháp: Sử dụng công thức tính thể tích hình hộp và thể tích hình trụ.
Cách giải: Thể tích nước trong bể khi đầy là
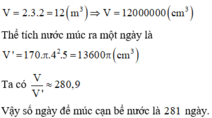

Theo giả thiết thể tích khối cầu đá bằng 3 8 - 1 8 = 1 4 thể tích khối trụ.
Do vậy ![]()
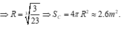
Chọn đáp án A.