Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = 3! = 6\)
- Gọi B là biến cố “Không lá thư nào được bỏ đúng phong bì”
A là biến cố “Có ít nhất một lá thư được bỏ đúng phong bì”
⇨ n(B) = 2
⇨ \(P(A) = 1 - P(B) = 1 - \frac{2}{6} = \frac{2}{3}\)

Đáp án A
Phương pháp giải: Áp dụng nguyên lý bù trừ trong bài toán xác suất
Lời giải:
Ta tính xác suất để xảy ra không một lá thư nào đúng địa chỉ.
Mỗi phong bì có 4 cách bỏ thư vào nên có tất cả 4! cách bỏ thư.
Gọi U là tập hợp các cách bỏ thư và Am là tính chất lá thư thứ m bỏ đúng địa chỉ.
Khi đó, theo công thức về nguyên lý bù trừ, ta có N ¯ = 4 ! - N 1 + N 2 - . . . + ( - 1 ) 4 N 4 .
Trong đó Nm ( 1 ≤ m ≤ 4 ) là số tất cả các cách bỏ thư sao cho có m lá thư đúng địa chỉ.
Nhận xét rằng, Nm là tổng theo mọi cách lấy m lá thư từ 4 lá, với mỗi cách lấy m lá thư, có (4 - m)! cách bỏ m lá thư này đúng địa chỉ, ta nhận được:
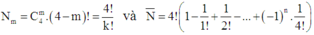
Suy ra xác suất cần tìm cho việc không lá thư nào đúng địa chỉ là
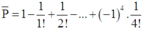
Vậy xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó là P = 1 - P ¯ = 5 8 .

Số cách bỏ 4 lá thư vào 4 bì thư là: ![]()
Kí hiệu 4 lá thư là: L1,L2,L3,L4 và bộ (L1L2L3L4) là một hóan vị của các số 1;2;3;4 trong đó ![]() nếu lá thư Li bỏ đúng địa chỉ.
nếu lá thư Li bỏ đúng địa chỉ.
Ta xét các khả năng sau
có 4 lá thư bỏ đúng địa chỉ:(1;2;3;4) nên có 1 cách bỏ
có 2 là thư bỏ đúng địa chỉ:
+) số cách bỏ 2 lá thư đúng địa chỉ là: ![]()
+) khi đó có 1 cách bỏ hai là thư còn lại
Nên trường hợp này có: ![]() cách bỏ.
cách bỏ.
Có đúng 1 lá thư bỏ đúng địa chỉ:
Số cách chọn lá thư bỏ đúng địa chỉ: 4 cách
Số cách chọn bỏ ba lá thư còn lại: cách
Nên trường hợp này có: cách bỏ.
Do đó: ![]()
Vậy .
.
Chọn A.

Đáp án C
Bỏ 4 lá thư vào 4 phong bì ta có số cách bỏ là. 4! Cách
Ta xét các trường hợp sau.
TH1: chỉ có một lá thư bỏ đúng.giải sử ta chọn 1 trong 4 lá để bỏ đúng (có 4 cách)
trong mỗi cách đó chọn một lá để bỏ sai (có 2 cách)
khi đó 2 lá còn lại nhất thiết là sai (1 cách)
vậy trong TH1 này có 4.2.1=8 cách.
TH2: có đúng 2 lá bỏ đúng
Tương tự trên, ta chọn 2 lá bỏ đúng (có C 4 2 = 6 cách)
2 lá còn lại nhất thiết sai (1 cách), vậy trong TH2 này có 6 cách.
TH3: dễ thấy khi 3 lá đã bỏ đúng thì đương nhiên là cả 4 lá đều đúng, vậy có 1 cách.
Suy ra có 8 + 6 +1 = 15 cách bỏ ít nhất có 1 lá thư vào đúng địa chỉ.
Vậy xác suất cần tìm là: 15 24 = 5 8

Đáp án C
Bỏ 4 lá thư vào 4 phong bì ta có số cách bỏ là. 4! Cách.
Ta xét các trường hợp sau
TH1: chỉ có một lá thư bỏ đúng. giải sử ta chọn 1 trong 4 lá để bỏ đúng (có 4 cách)
trong mỗi cách đó chọn một lá để bỏ sai (có 2 cách), khi đó 2 lá còn lại nhất thiết là sai (1 cách)
vậy trong TH1 này có 4.2.1 = 8 cách.
TH2: có đúng 2 lá bỏ đúng. Tương tự trên, ta chọn 2 lá bỏ đúng (có C 4 2 = 6 cách)
2 lá còn lại nhất thiết sai (1 cách), vậy trong TH2 này có 6 cách.
TH3: dễ thấy khi 3 lá đã bỏ đúng thì đương nhiên là cả 4 lá đều đúng, vậy có 1 cách.
Suy ra có 8+6+1=15 cách bỏ ít nhất có 1 lá thư vào đúng địa chỉ.
Vậy xác suất cần tìm là: 15 24 = 5 8

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)
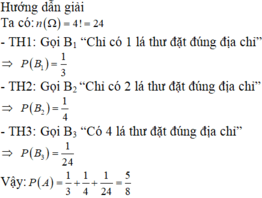
Đáp án D
Số phần tử không gian mẫu là: n ( Ω ) = 3 ! = 6 .
Gọi A là biến cố “Có ít nhất một lá thư được bỏ đúng phong bì”.
Ta xét các trường hợp sau:
Nếu lá thứ nhất bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.
Nếu lá thứ hai bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.
Nếu lá thứ ba bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.
Không thể có trường hợp hai lá thư bỏ đúng và một lá thư bỏ sai.
Cả ba lá thư đều được bỏ đúng có duy nhất 1 cách.
⇒ n A = 4
Vậy xác suất để có ít nhất một lá thư được bỏ đúng phong bì là:
P ( A ) = n ( A ) n Ω = 4 6 = 2 3 .
Cách 2:
Gọi B là biến cố “Không có lá thư nào được bỏ đúng phong bì”.
⇒ n B = 2
P ( A ) = 1 - P ( B ) = 1 - n ( B ) n Ω = 1 - 2 6 = 2 3 .