Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Công suất tiêu thụ của mạch:
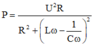
với U = k ω , k là hệ số tỉ lệ
Biến đổi toán học, ta thu được:
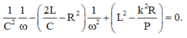
Hai giá trị của tần số góc cho cùng công suất tiêu thụ trên mạch thỏa mãn:
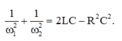
+ Với ω = 2 πn thay các giá trị vào phương trình trên ta tìm được L ≈ 0 , 63 H

f1=\(\frac{n_1}{60}\).2=45HZ ω1=2πf1=90π(rad/s)
f2=\(\frac{n_2}{60}\).2=60HZ ω2=2πf2=120π(rad/s)
P1=P2
\(\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{C1}\right)^2}}=\frac{\frac{4}{3}U}{\sqrt{R^2+\left(Z_{L2}-Z_{C2}\right)^2}}\) thay so tim duoc L=0,477 Dap an:C
Giải:
\(I=\dfrac{U}{Z}=\dfrac{E}{Z}\) với \(E\) là suất điện động hiệu dụng giữa hai cực máy phát:
\(E=\sqrt{2}\omega N\Phi_0=\sqrt{2}2\pi fN\Phi_0=U\left(r=0\right)\)
Với \(f=np:\) \(n\) tốc độ quay của roto, \(p\) số cặp cực từ
\(\Rightarrow f_1=\dfrac{1350.2}{60}=\dfrac{135}{3}Hz\) \(\Rightarrow\omega_1=90\pi;Z_{C1}=20\Omega\)
\(\Rightarrow f_2=\dfrac{1800.2}{60}=60Hz\) \(\Rightarrow\omega_2=120\pi;Z_{C2}=15\Omega\)
\(P_1=P_2\Leftrightarrow I_1=I_2\)
\(\Leftrightarrow\dfrac{\omega_1^2}{R^2+\left(\omega_1L-\dfrac{1}{\omega_1C}\right)^2}=\) \(\dfrac{\omega_2^2}{R^2+\left(\omega_2L-\dfrac{1}{\omega_2C}\right)^2}\)
\(\Rightarrow\dfrac{90^2}{R^2+\left(\omega_1L-20\right)^2}=\dfrac{120^2}{R^2+\left(\omega_2L-15\right)^2}\)
\(\Rightarrow\dfrac{9}{R^2+\left(\omega_1L-20\right)^2}=\dfrac{16}{R^2+\left(\omega_2L-15\right)^2}\)
\(\Leftrightarrow9\left[R^2+\left(\omega_2L-15\right)^2\right]\) \(=16\left[R^2+\left(\omega_1L-20\right)^2\right]\)
\(\Leftrightarrow-7R^2+\left(9\omega_2^2-16\omega_1^2\right)L^2-\) \(\left(270\omega_2-640\omega_1\right)L\) \(+9.15^2-16.20^2=0\)
\(\Leftrightarrow\left(9\omega_2^2-16\omega_1^2\right)L^2-\left(270\omega_2-640\omega_1\right)L\) \(-7R^2+9.15^2\)\(-16.20^2=0\)
\(\Leftrightarrow25200\pi L=37798,67\Rightarrow L=0,48H\)
Vậy ta chọn đáp án \(C\)

+ Suất điện động hiệu dụng giữa hai cực
máy phát điện là
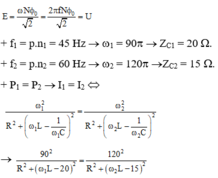
® (9w22 - 16w12)L2 - (270w2 - 640w1)L - 7R2 + 9.152 - 16.202 = 0
+ Thay w1, w2 và R vào phương trình trên ta được L = 0,48 H.

Đáp án B
+ Máy phát điện có E tỉ lệ thuận với ![]()
Có ![]()
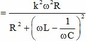
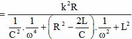
Để P max thì mẫu số phải min. Để ý thấy mẫu số là dạng tam thức bậc 2, nên mẫu số min khi và chỉ khi ![]()
Mặt khác, có 2 giá trị
ω
1
và
ω
2
làm P bằng nhau nên chúng sẽ thỏa mãn định lý Viete: 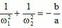
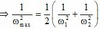
Có ![]()
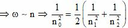
![]() (vòng/phút)
(vòng/phút)

Tần số góc là:
\(w=\frac{720.2\pi}{60}=25\pi\)
Suất điện động cực đại là:
\(\Rightarrow E_0=N.B.S.w=200\frac{25.10^{-3}}{\pi}.4=500V\)
Suất điện động hiệu dụng là:
\(E=\frac{E_0}{\sqrt{2}}=250\sqrt{2V}\)

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V



Đáp án A
+ Công suất tiêu thụ của mạch: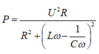
với U = k ω , k là hệ số tỉ lệ. Biến đổi toán học, ta thu được:
Hai giá trị của tần số góc cho cùng công suất tiêu thụ trên mạch thỏa mãn:
+ Với ω = 2 π n thay các giá trị vào phương trình trên ta tìm được L ≈ 0 , 63 H