Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
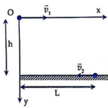
Chọn hệ trục tọa độ Oxy có gốc O tại vị trí máy bay khi cắt bom, Ox hướng theo , Oy hướng thẳng xuống dưới. Gốc thời gian lúc cắt bom
- Các phương trình chuyển động của máy bay là
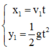
-Các phương trình chuyển động của tàu chiến là
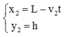
- Khi gặp nhau: x1 = x2; y1 = y2
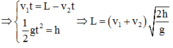

Chọn A.
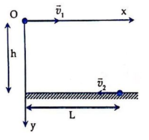
Chọn hệ trục tọa độ Oxy có gốc O tại vị trí máy bay khi cắt bom, Ox hướng theo v 1 ⇀ , Oy hướng thẳng xuống dưới. Gốc thời gian lúc cắt bom.



Bom là vật ném theo phương ngang ở độ cao h. Áp dụng phương pháp tọa độ với hệ trục Oxy như hình vẽ
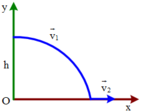
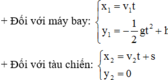


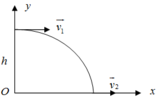
v 1 = 504 k m / h = 140 m / s , v 2 = 90 k m / h = 25 m / s
Bom là vật ném theo phương ngang ở độ cao h. Áp dụng phương pháp tọa độ với hệ trục Oxy như hình vẽ.
a. Máy bay và tàu chuyển động cùng chiều:
Đối với máy bay x 1 = v 1 t y 1 = − 1 2 g t 2 + h
Đối với tàu chiến x 2 = v 2 t + s y 2 = 0
Để bom thả trúng tàu thì: x 2 = x 1 ; y 2 = y 1
⇒ − 1 2 g t 2 + h = 0 v 1 t = v 2 t + s ⇒ t = 2 h g ⇒ s = v 1 − v 2 t
Vậy máy bay cách tàu chiến một quãng đường là:
s = v 1 − v 2 2 h g = 140 − 25 . 2.2000 10 = 2300 m = 2 , 3 k m
b. Máy bay và tàu chuyển động ngược chiều.
Chứng minh tương tự câu a ta có
⇒ s = v 1 + v 2 2 h g = 140 + 25 . 2.2000 10 = 3300 m = 3 , 3 k m

Bài 1 :
P1 =m1g => m1 = 1(kg)
P2 = m2g => m2 =1,5(kg)
Trước khi nổ, hai mảnh của quả lựu đạn đều chuyển động với vận tốc v0, nên hệ vật có tổng động lượng : \(p_0=\left(m_1+m_2\right)v_0\)
Theo đl bảo toàn động lượng : \(p=p_0\Leftrightarrow m_1v_1+m_2v_2=\left(m_1+m_2\right)v_0\)
=> \(v_1=\frac{\left(m_1+m_2\right)v_0-m_2v_2}{m_1}=\frac{\left(1+1,5\right).10-1,5.25}{1}=-12,5\left(m/s\right)\)
=> vận tốc v1 của mảnh nhỏ ngược hướng với vận tốc ban đầu v0 của quả lựu đạn.
Bài2;
Vận tốc mảnh nhỏ trước khi nổ là :
v02=\(v_1^2=2gh\)
=> v1 = \(\sqrt{v_0^2-2gh}=\sqrt{100^2-2.10.125}=50\sqrt{3}\left(m/s\right)\)
Theo định luật bảo toàn động lượng :
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
p = mv = 5.50 =250(kg.m/s)
\(\left\{{}\begin{matrix}p_1=m_1v_1=2.50\sqrt{3}=100\sqrt{3}\left(kg.m/s\right)\\p_2=m_2v_2=3.v_2\left(kg.m/s\right)\end{matrix}\right.\)
+ Vì \(\overrightarrow{v_1}\perp\overrightarrow{v_2}\rightarrow\overrightarrow{p_1}\perp\overrightarrow{p_2}\)
=> p2 = \(\sqrt{p_1^2+p^2}=\sqrt{\left(100\sqrt{3}\right)^2+250^2}=50\sqrt{37}\left(kg.m/s\right)\)
=> v2= \(\frac{p_2}{m_2}=\frac{50\sqrt{37}}{3}\approx101,4m/s+sin\alpha=\frac{p_1}{p_2}=\frac{100\sqrt{3}}{50\sqrt{3}}\)
=> \(\alpha=34,72^o\)

1/ Đáp án B
2/
a) Thời gian vật rơi:
\(t=\frac{v}{g}=3\left(s\right)\)
- Độ cao thả vật:
\(h=\frac{1}{2}gt^2=45\left(m\right)\)
b) Quãng đường vật rơi trong giây cuối cùng trước khi chạm đất :
\(\Delta s'=s_3-s_2=25\left(m\right)\)
1.B
2. a) h=\(\dfrac{v^2}{2g}\)=\(\dfrac{30^2}{2.10}\)=45(m)
t=\(\dfrac{v}{g}\)=\(\dfrac{30}{10}\)=3(s)
b) S2s=\(\dfrac{1}{2}\)gt2s2=\(\dfrac{1}{2}\).10.22=20(m)
\(\Delta S\)=S3s-S2s=h-S2s=25(m)
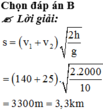
Đáp án B.
Chọn hệ trục tọa độ Oxy có gốc O tại vị trí máy bay khi cắt bom, Ox hướng theo v 1 → , Oy hướng thẳng đứng xuống dưới. Gốc thời gian lúc cắt bom.