Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) dạng quỹ đạo của vật là 1 nhánh parabol
b) thời gian trong không khí
h=0,5.g.t2\(\Rightarrow\)t=3s
c) tầm xa
l=vo.t=60m
d)vận tôc skhi chạm đất
\(v=\sqrt{v_0^2+\left(g.t\right)^2}\)=\(5\sqrt{61}\)m/s

a. Theo phương \(Ox\) có: \(x=v_0t=10t\)
Theo phương \(Oy \) có: \(y=\frac{gt^2}{2}=5t^2\)
Phương trình quỹ đạo của vật là
\(y=\frac{g}{2v_0^2}x^2=\frac{x^2}{20}\)
b. Tầm bay xa của vật là
\(L=v _0t=v_0\sqrt{\frac{2h}{g}}=10.\sqrt{\frac{2.50}{10}}=31,6\) m
c. Vận tốc của vật khi chạm đất là
\(v=\sqrt{2gh}=\sqrt{2.10.50}=31,6\) m/s

phương trình quỹ đạo của vật là
y=\(\dfrac{1}{2}\dfrac{g}{v_0^2}.x\)=\(\dfrac{1}{20}.x\)

a/ Vì ném ngang nên vận tốc ban đầu theo phương y bằng 0
\(\Rightarrow y=h+v_{0y}t+\frac{1}{2}gt^2=5t^2\)
\(\Rightarrow x=v_{0x}t=20t\)
b/ \(v_y=v_{0y}+gt=10.1=10\left(m/s\right)\)
\(v_x=v_{0x}=20\left(m/s\right)\)
\(\Rightarrow v=\sqrt{v_x^2+v_y^2}=\sqrt{10^2+20^2}=10\sqrt{5}\left(m/s\right)\)
Cách khác :
\(v_o=20\frac{m}{s},h=45m\)
a . Phương trình quỹ đạo chuyển động:
\(y=\frac{g}{2.v_o^2}x^2\)
b . \(t=1s\)
Vận tốc của vật khi đi được 1s
\(v=\sqrt{v_o^2+\left(gt\right)^2}=\sqrt{20^2+\left(10.1\right)^2}=10\sqrt{5}\frac{m}{s}\)

Bài 1 :
P1 =m1g => m1 = 1(kg)
P2 = m2g => m2 =1,5(kg)
Trước khi nổ, hai mảnh của quả lựu đạn đều chuyển động với vận tốc v0, nên hệ vật có tổng động lượng : \(p_0=\left(m_1+m_2\right)v_0\)
Theo đl bảo toàn động lượng : \(p=p_0\Leftrightarrow m_1v_1+m_2v_2=\left(m_1+m_2\right)v_0\)
=> \(v_1=\frac{\left(m_1+m_2\right)v_0-m_2v_2}{m_1}=\frac{\left(1+1,5\right).10-1,5.25}{1}=-12,5\left(m/s\right)\)
=> vận tốc v1 của mảnh nhỏ ngược hướng với vận tốc ban đầu v0 của quả lựu đạn.
Bài2;
Vận tốc mảnh nhỏ trước khi nổ là :
v02=\(v_1^2=2gh\)
=> v1 = \(\sqrt{v_0^2-2gh}=\sqrt{100^2-2.10.125}=50\sqrt{3}\left(m/s\right)\)
Theo định luật bảo toàn động lượng :
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
p = mv = 5.50 =250(kg.m/s)
\(\left\{{}\begin{matrix}p_1=m_1v_1=2.50\sqrt{3}=100\sqrt{3}\left(kg.m/s\right)\\p_2=m_2v_2=3.v_2\left(kg.m/s\right)\end{matrix}\right.\)
+ Vì \(\overrightarrow{v_1}\perp\overrightarrow{v_2}\rightarrow\overrightarrow{p_1}\perp\overrightarrow{p_2}\)
=> p2 = \(\sqrt{p_1^2+p^2}=\sqrt{\left(100\sqrt{3}\right)^2+250^2}=50\sqrt{37}\left(kg.m/s\right)\)
=> v2= \(\frac{p_2}{m_2}=\frac{50\sqrt{37}}{3}\approx101,4m/s+sin\alpha=\frac{p_1}{p_2}=\frac{100\sqrt{3}}{50\sqrt{3}}\)
=> \(\alpha=34,72^o\)

Đáp án C
Phương trình quỹ đạo của vật là y = g x 2 2 v 0 2 = 10. x 2 2.10 2 = 0 , 05 x 2


a. Chọn hệ quy chiếu Oxy như hình vẽ
Thời điểm ban đầu
Chiếu lên trục ox có
x 0 = 0 ; v 0 x = v 0 c o s α = 10 2 ( m / s )
Chiếu lên trục oy có
y 0 = 0 ; v 0 y = v 0 s i n α = 10 √ 2 ( m / s )
Xét tại thời điểm t có a x = 0 ; a y = - g
Chiếu lên trục ox có
v x = 10 √ 2 ( m / s ) ; x = 10 √ 2 t
Chiếu lên trục Oy có
v y = 10 √ 2 - 10 t ; y = 45 + 10 √ 2 t - 5 t 2
⇒ y = 45 + x - x 2 40 Vậy vật có quỹ đạo là một Parabol
Khi lên đến độ cao max thì: v y = 0 ⇒ 0 = 10 √ 2 - 10 t ⇒ t = √ 2 ( s )
H m a x = y = 45 + 10 . √ 2 . √ 2 - 5 ( √ 2 ) 2 = 55 ( m )
Khi vật chạm đất thì y = 0 ⇒ 45 + 10 √ 2 t - 5 t 2 = 0 ⇒ t = 4 , 73 ( s )
Vậy sau 4,73s thì vật chạm đất
b. Tầm xa của vật L = x = 10 √ 2 . 4 , 73 ≈ 66 , 89 ( m )
Vận tốc vật khi chạm đất v = v x 2 + v y 2
Với v y = 10 √ 2 - 10 . 4 , 73 = 33 , 16 ( m / s )
⇒ v = √ ( ( 10 √ 2 ) 2 + 33 , 〖 16 〗 2 ) = 36 , 05 ( m / s )
c. Khi vật có độ cao 50 thì
y = 50 = 45 + 10 √ 2 t - 5 t 2 ⇒ t 1 = 2 , 414 ( s ) ; t 2 = 0 , 414 ( s )
Lúc t 1 = 2 , 414 ( s ) ⇒ v 1 = 10 √ 2 - 10 t 1 = 10 √ 2 - 10 . 2 , 414 ≈ - 10 ( m / s )
Lúc t 2 = 0 , 414 ( s ) ⇒ v 2 = 10 √ 2 - 10 t 2 = 10 √ 2 - 10 . 0 , 414 ≈ 10 ( m / s )
Ứng với hai trường hợp vật đi xuống đi lên
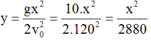
Đáp án B
Ta có phương trình quỹ đạo y = g x 2 2 v 0 2 = 10. x 2 2.120 2 = x 2 2880