Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2/ Khi vật đặt cách mắt 20 cm thì d = 20 cm, lúc này ảnh của vật qua thấu kính mắt (thủy tinh thể) không hiện trên võng mạc, để nhìn rõ người này phải điều tiết mắt để ảnh hiện trên đúng võng mạc nên d' = OV.
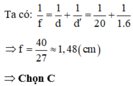

Chọn A
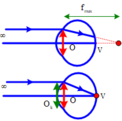
+ Độ tụ của hệ thấu kính ghép sát:
D = D M + D k
⇔ 1 f = 1 f M + 1 f k
+ Sau khi ghép tiêu điểm phải nằm đúng trên võng mạc:
→ f M = f max = 0 , 015 f = O V = 0 , 0152 1 0 , 0152 = 1 0 , 015 + D K ⇒ D K = − 0 , 88 d p

Chọn B
D min = 1 f max = 1 O C V + 1 O V D max = 1 f min = 1 O C C + 1 O V ⇒ 1 1 , 5 = 1 O C V + 1 1 , 52 1 1 , 415 = 1 O C C + 1 1 , 52 ⇒ O C V = 114 O C C = 20 , 48
⇒ C C C V = O C V − O C C = 93 , 52 c m

Chọn D
Khi quan sát một vật cách mắt:
D = 1 d + 1 O V = 1 0 , 2 + 1 2 , 2.10 − 2 = 50 , 45 d p

Chọn A
D min = 1 f max = 1 O C V + 1 O V D max = 1 f min = 1 O C C = 1 O V ⇒ 1 1 , 6 = 1 O C V + 1 1 , 62 1 1 , 536 = 1 O C C + 1 1 , 62 ⇒ O C V = 129 , 6 c m O C C = 27 , 54 c m
+ Sơ đồ tạo ảnh:
A B ⎵ d ∈ d C ; d V → O 1 A 1 B 1 ⎵ d / d M ∈ O C C ; O C V → M a t V 1 d C + 1 − O C C = D K 1 d V + 1 − O C V = D K
⇒ 1 d C + 1 − O C C = 1 d V + 1 − O C V → O C C = 27 , 54 ; O C V = 129 , 6 d V = ∞ d C = 35 c m

a) Số bội giác của ảnh: \(G_{\infty}=\dfrac{\delta.OC_C}{f_1.f_2}=\dfrac{16.20}{1.4}=80\)
b) * Xét TH quan sát ở điểm cực viễn: (nhắm chừng vô cực)
d2'= -OCv= - vô cùng
l= f1+f2+ $ =21 cm ($: là độ dài quang học nhá bạn)
=>1/f2= 1/d2+ 1/d2' ( vì d2'= - vô cùng)
=> f2=d2=4 cm
=>d1'= l-d2=21-4=17 cm
=>d1= (d1'*f1)/(d1'-f1)=1.0625 cm
Ta có k=-d1'/d1=-16 =>|k|=16
Ta có: k= A1'B1'/ AB=
=> A1'B1'= |k|AB
tan@= A1'B1'/f2 = |k|AB/f2 (@ là góc trong ảnh đó bạn, cái này áp dụng hệ thức lượng trong tam giác vuông)
=> AB= tan@*f2/ |k|
=>AB= (tan 2' * 4)/ 16=0.0001454 m
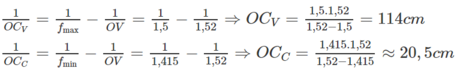
1/ Khoảng cách từ quang tâm của thủy tinh thể đến võng mạc là: d ' = O V = 1 , 6 c m
+ Khi mắt không điều tiết tức là nhìn vật ở vô cực d = O C v = ∞ lúc này ảnh qua thấu kính mắt hiện đúng trên võng mạc (màng lưới). Ta có: