Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Sử sụng hệ thức: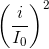 
+
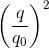= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω =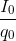 
= 50 (rad/s)
mình bị nhầm ở đáp án
A. \(\frac{4}{3}\mu s\) các câu khác cũng như vậy nhé
Năng lượng của mạch dao động W = \(\frac{Q_0^2}{2C}=\frac{LI^2_0}{2}\) → chu kì dao động của mạch
\(T=2\pi\sqrt{LC}=2\pi\frac{Q_0}{I_0}=16.10^{-6}\left(s\right)=16\mu s\).Thời gian điện tích giảm từ Q0 dến Q0/2
q = Q0cos \(\frac{2\pi}{T}t=\frac{Q_0}{2}\rightarrow\frac{2\pi}{T}t=\frac{\pi}{3}\rightarrow t=\frac{T}{6}=\frac{8}{3}\mu s\)
→ C
Từ ĐK đầu bài ta có:
tần số dao động riwwng của mạch là:
giải phương trình bâc 2 này ra ta được:
Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng
Dòng điện đổi chiều khi dòng điện đi qua VTCB.
Vẽ đường tròn tương ứng
-60 x 0 N M 150
Vị trí ban đầu ứng với pha ban đầu là \(-\frac{\pi}{3}\) ứng với điểm N.
Vị trí gần nhất (quay theo chiều ngược chiều kim đồng hồ) thì điểm N là vị trí gần nhất tại đó dòng đổi chiều.
\(t=\frac{\varphi}{\omega}=\frac{5\pi}{6}\Rightarrow\omega=\frac{5\pi}{6}:t=2\pi.10^6\)
Điện tích cực đại \(Q_o=\frac{I_0}{\omega}=\frac{30}{2\pi.10^6}=\frac{1,5.10^{-5}}{\pi}C\)
Như vậy đáp án C thỏa mãn.
\(C = \frac{1}{\omega^2.L}= 5.10^{-6}F.\)
\(U_0 = \frac{q_0}{C}= \frac{I_0}{C.\omega}= \frac{I_0.\sqrt{L}}{\sqrt{C}} = 8V.\)
\(i = I = \frac{I_0}{\sqrt{2}}. \)
\(\left(\frac{u}{U_0}\right)^2+\left(\frac{i}{I_0}\right)^2=1\)
=> \(\left(\frac{u}{U_0}\right)^2 = 1- \left(\frac{i}{I_0}\right)^2 = 1 - \frac{1}{2}= \frac{1}{2}\)
=> \(u = \frac{1}{\sqrt{2}}U_0= 4\sqrt{2}V.\)
Bạn nên gửi mỗi câu hỏi một bài thôi để mọi người tiện trao đổi.
1. \(Z_L=200\sqrt{3}\Omega\), \(Z_C=100\sqrt{3}\Omega\)
Suy ra biểu thức của i: \(i=1,1\sqrt{2}\cos\left(100\pi t-\frac{\pi}{3}\right)A\)
Công suất tức thời: p = u.i
Để điện áp sinh công dương thì p > 0, suy ra u và i cùng dấu.
Biểu diễn vị trí tương đối của u và i bằng véc tơ quay ta có:
u u i i 120° 120°
Như vậy, trong 1 chu kì, để u, i cùng dấu thì véc tơ u phải quét 2 góc như hình vẽ.
Tổng góc quét: 2.120 = 2400
Thời gian: \(t=\frac{240}{360}.T=\frac{2}{3}.\frac{2\pi}{100\pi}=\frac{1}{75}s\)
2. Khi nối tắt 2 đầu tụ điện thì cường độ dòng điện hiệu dụng không đổi \(\Rightarrow Z_1=Z_2\Leftrightarrow Z_C-Z_L=Z_L\Leftrightarrow Z_C=2Z_L\)
\(U_C=1,2U_d\Leftrightarrow Z_C=2Z_d\Leftrightarrow Z_C=2\sqrt{R^2+Z_L^2}\)
\(\Leftrightarrow2Z_L=\sqrt{R^2+Z_L^2}\Leftrightarrow R=\sqrt{3}Z_L\)
Khi bỏ tụ C thì cường độ dòng điện của mạch là: \(I=\frac{U}{Z_d}=\frac{U}{\sqrt{R^2+Z_L^2}}=\frac{220}{\sqrt{3.Z_L^2+Z_L^2}}=0,5\)
\(\Rightarrow Z_L=220\Omega\)
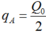
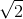
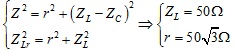
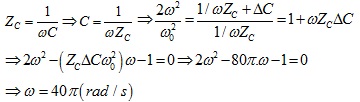
Đáp án B
Phương pháp: Sử dụng công thức tính thời gian bằng đường tròn.
Cách giải:Ta có phương trình điện tích :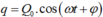
Ban đầu bản A tích điện ½ Q0 và đang tăng nênpha ban đầu có giá trị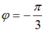
Khi bản B có điện tích cực đại Q0 thì bản A có điện tích –Q0. Ta có vecto quay như hình vẽ:
Ta có: