Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

Phần diện tích trồng cây cảnh chiếm
1-3/5-24%=4/25 ( diện ích mảnh đất)
* Diện tích mảnh đất là:
24:4/25=150 ( m2)
Diện tích đất để làm nhà là:
150.3/5=90 ( m2)
Đáp số: Diện tích mảnh đất: 150 m2
Diện tích làm nhà: 90 m2

1. Một khu đồi trồng cây ăn quả có tất cả 1950 cây, gồm các loại cam, quýt và vải thiều. Biết \(\dfrac{2}{3}\) số cây cam bằng \(\dfrac{3}{5}\) cây quýt và bằng \(\dfrac{6}{7}\) số cây vải thiều. Tính xem mỗi loại có bao nhiêu cây.
\(\dfrac{2}{3}\) số cây cam bằng \(\dfrac{3}{5}\) cây quýt và bằng \(\dfrac{6}{7}\) số cây \(\Rightarrow\) \(\dfrac{6}{9}\) số cây cam bằng \(\dfrac{6}{10}\) cây quýt và bằng \(\dfrac{6}{7}\) số cây vải thiều
Ta có sơ đồ:
Cam |-------|-------|-------|-------|-------|-------|-------|-------|-------| (9 phần)
Quýt |-------|-------|-------|-------|-------|-------|-------|-------|-------|-------| (10 phần)
Vải |-------|-------|-------|-------|-------|-------|-------| (7 phần)
Số cây cam là:
\(1950:\left(9+10+7\right).9=675\) (cây)
Số cây quýt là:
\(1950:\left(9+10+7\right).10=750\) (cây)
Số cây vải thiều là:
\(1950:\left(9+10+7\right).7=525\) (cây)
Đáp số: Quýt: 675 cây
Quýt: 750 cây
Vải: 525 cây
2. Một mảnh đất được chia thành 3 phần. Phần để xây nhà có diện tích chiếm \(\dfrac{3}{5}\) diện tích mảnh đất. Phần để làm sân có diện tích bằng 24% diện tích mảnh đất, phần diện tích còn lại là 24m2 để trồng cây cảnh.
a) Tính diện tích mảnh đất
Phân số chỉ phần diện tích còn lại để trồng cây cảnh là:
\(1-\dfrac{3}{5}-24\%=\dfrac{4}{25}\) (tổng số đất)
Diện tích mảnh đất là:
\(24:\dfrac{4}{25}=150m^2 \)
b) Tính diện tích phần đất để làm nhà
Diện tích phần đất để làm nhà là:
\(150.\dfrac{3}{5}=90m^2\)
Đáp số: a) \(150m^2\)
b) \(90m^2\)

b,(*)chứng minh a=-3b:
xét a-b=2(a+b)
=>a-b=2a+2b
=>-b-2b=2a-a
=>-3b=a (đpcm)
(*) tính a/b :
Từ -3b=a=>a/b=-3
(*)tính a và b:
Ta có : a-b=a/b=-3
và 2(a+b)=a/b=-3
hệ pt<=>a-b=-3
và 2(a+b)=-3
<=>a-b=-3 (1)
và a+b=-1,5 (2)
Lấy (1)+(2),vế theo vế ta đc:
(a-b)+(a+b)=-3+(-1,5)
=>a-b+a+b=-4,5
=>2a=-4,5=>a=-2,25
Mà a-b=-3=>b=0,75
Vậy (a;b)=(-2,25;0,75)
c) vì (x-y2+z)2 >= 0 với mọi x;y;z
(y-2)2 >= 0 với mọi y
(z+3)2 >= 0 với mọi z
=>(x-y2+z)2+(y-2)2+(z+3)2 >= 0 với mọi x;y;z
Mà theo đề: (x-y2+z)2+(y-2)2+(z+3)2=0
=>(x-y2+z)2=(y-2)2=(z+3)2=0
+)(y-2)2=0=>y=2
+)(z+3)2=0=>z=-3
Thay y=2;z=-3 vào (x-y2+z)2=0=>x-22+(-3)2=0=>x=-5
Vậy (x;y;z)=(-5;2;-3)

Câu 1:
\(AB=\sqrt{\left[3-\left(-2\right)\right]^2+\left(3-2\right)^2}=\sqrt{26}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(-2-3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-2-2\right)^2}=4\sqrt{2}\)
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{2\sqrt{26}+4\sqrt{2}}{2}=\sqrt{26}+2\sqrt{2}\)
\(S=\sqrt{\left(\sqrt{26}+2\sqrt{2}\right)\cdot2\sqrt{2}\cdot2\sqrt{2}\cdot\left(\sqrt{26}-2\sqrt{2}\right)}=\sqrt{18\cdot8}=12\left(đvdt\right)\)

n6 - n4 + 2n3 + 2n2
= n2 . (n4 - n2 + 2n +2)
= n2 . [n2(n - 1)(n + 1) + 2(n + 1)]
= n2 . [(n + 1)(n3 - n2 + 2)]
= n2 . (n + 1) . [(n3 + 1) - (n2 - 1)]
= n2. (n + 1)2 . (n2 - 2n + 2)
Với n ∈ N, n > 1 thì n2 - 2n + 2 = (n - 1)2 + 1 > (n - 1)2
Và n2 - 2n + 2 = n2 - 2(n - 1) < n2
Vậy (n - 1)2 < n2 - 2n + 2 < n2
=> n2 - 2n + 2 không phải là một số chính phương.

a)Ta xét trong tam giác ABH có Góc H =90độ
=>BAHˆ+ABHˆ=90
mà BAHˆ+HACˆ=90=A^(gt)
=>ABHˆ=HACˆ
Xét tam giác BHA và Tam giác AIC có:
AB=AC(gt)
H^=AICˆ=90(gt)
ABHˆ=HACˆ(c/m trên)
=>Tam giác BHA=Tam giác AIC(cạnh huyền-góc nhọn)
=>BH=AI(hai cạnh tương ứng)
b)Vì Tam giác BHA=Tam giác AIC(c/m trên)
=>IC=AH(hai cạnh tương ứng)
Xét trong tam giác vuông ABH có:
BH2+AH2=AB2
mà IC=AH
=>BH2+IC2=AB2(th này là D nằm giữa B và M)
Ta có thể c/m tiếp rằng D nằm giữa M và C thì ta vẫn c/m được Tam giác BHA=Tam giác AIC(cạnh huyền-góc nhọn) và BH2+IC2=AC2=AB2
=>BH2+CI2 có giá trị ko đổi
c)Ta xét trong tam giác DAC có IC,AM là 2 đường cao và cắt nhau tại N(AM cũng là đường cao do là trung tuyến của tam giác cân xuất phát từ đỉnh và cũng chính là đường cao của đỉnh đó xuống cạnh đáy=>AM vuông góc với DC)
=>DN chính là đường cao còn lại=>DN vuông góc với AC(là cạnh đối diện đỉnh đó)
d)Ta dễ dàng tính được Tam giác DMN cân tại M=>DM=MN(dựa vào số đo của các góc và 1 số c/m trên)
Từ M kẻ đường thẳng ME vuông góc với AD còn MF vuông góc với IC,Ta dễ dàng c/m được tam giác MED=Tam giác MFN(cạnh huyền-góc nhọn)
=>ME=MF(là hai đường vuông góc tại điểm M gióng xuống hai cạnh của góc HICˆ)
Theo tính chất của đường phân giác(Điểm nằm trên đường phân giác của góc này thì cách đều hai cạnh tạo thành góc đó)=>IM là tia phân giác của HICˆ
Đáp án A
Phương pháp:
- Xác định góc giữa mặt phẳng và mặt phẳng.
- Lập tỉ lệ thể tích thông qua tỉ lệ diện tích đáy và tỉ lệ chiều cao.
Cách giải:
Xét hình nón (H) thỏa mãn yêu cầu đề bài, có một thiết diện qua trục là tam giác SAB.
Ta có: SAB cân tại S và là tam giác vuông cân => △ SAB vuông cân tại đỉnh S
Gọi O là trung điểm của AB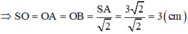
Thể tích hình nón (H):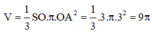
Gọi (P) là một mặt phẳng đi qua đỉnh và tạo với đáy một góc 600 thiết diện của (P) với mặt đáy là tam giác cân SMN.
Gọi I là trung điểm của MN (hiển nhiên I không trùng O), suy ra IO ⊥ MN. Mà SO ⊥ MN
Tam giác SIO vuông tại O
Gọi V0 là thể tích của phần nhỏ hơn. Ta có: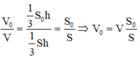
*) Tính diện tích đáy của phần có thể tích nhỏ hơn:
Diện tích hình tròn
Đặt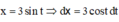
Đổi cận: