Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
Chọn ngẫu nhiên 4 đại biểu có: C 20 4 cách chọn.Chọn ra 4 đại biểu có đủ 3 nước dẫn đến 3 trường hợp:
1) 2A – 1B – 1C, 1A – 2B – 1C, 1A – 1B – 2C dẫn đến có C 6 2 . 7 . 7 + 6 . C 7 2 . 7 + 6 . 7 . C 7 2 = 2499 cách.
2) Xét bài toán chọn 4 đại biểu đủ cả 3 nước mà toàn nam, dẫn đến các trường hợp:2A – 1B – 1C, 1A – 2B – 1C, 1A – 1B – 2C được C 4 2 . 5 . 5 + 4 . C 5 2 . 5 + 4 . 5 . C 5 2 = 550 cách.
3) Xét bài toán chọn 4 người đủ cả 3 nước toàn nữ: tương tự ta được 12 cách.
4) Vậy số trường hợp chọ được 4 đại biểu để mỗi nước đều có ít nhất một đại viểu và có cat đại biểu nam và đại biểu nữ là: 2499 – 550 – 12 = 1937
Vậy P= 1937 4845
Đáp án A
Có 2 trường hợp như sau
+)TH1: có 3 nam, 2 nữ, suy ra có 
cách chọn
+) TH2: có 4 nam, 1 nữ, suy ra có 
cách chọn
Suy ra xác suất cần tính bằng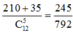 
Đáp án A
Bạn Nam chọn 3 trong 10 câu nên n Ω = C 10 3 = 120.
Gọi A là biến cố “Nam chọn ít nhất một câu hình học”.
Khi đó A ¯ : “Nam không chọn được câu hình học nào” hay Nam chỉ chọn toàn câu đại số
⇒ n A ¯ = C 6 3 = 20 ⇒ n A = n Ω − n A ¯ = 100 ⇒ P A = 100 120 = 5 6
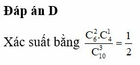
Đáp án đúng : D